题目内容
求证：
+
＞3+
．
| 5 |
| 7 |
| 3 |
考点：不等式的证明
专题：推理和证明
分析：利用分析法，从要证的结论入手，寻找使结论成立的充分条件，直到找到这样的充分条件，即可证得原结论成立．
解答：
证明：要证明
+
＞3+
，
只需证明：（
+
）2＞（3+
）2，
即证：12+2
＞12+6
，
也就是证明
＞3
=
，该式显然成立，
以上步步可逆，
故原不等式成立．
| 5 |
| 7 |
| 3 |
只需证明：（
| 5 |
| 7 |
| 3 |
即证：12+2
| 35 |
| 3 |
也就是证明
| 35 |
| 3 |
| 27 |
以上步步可逆，
故原不等式成立．
点评：本题考查不等式的证明，着重考查分析法证明不等式，考查推理证明能力，是基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
直线xtan
+y+2=0的倾斜角α是（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知a=(
)
，b=(
)
，c=log
，则a，b，c之间的大小关系为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a＞b＞c |
| B、c＞a＞b |
| C、a＞c＞b |
| D、c＞b＞a |
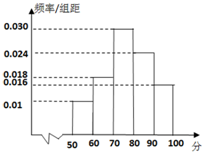某校为了解高一年段期中考试数学科的情况，从高一的所有数学试卷中随机抽取n份试卷进行分析，得到数学成绩频率分布直方图如下图，其中成绩在[70，80）的人数为15，规定：成绩≥80分为优秀．
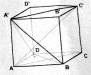在正方体ABCD-A′B′C′D′中，求证：