题目内容
当x>0时,下列函数中最小值为2的是( )
A、y=x+
| ||
| B、y=x2-2x+3 | ||
C、y=
| ||
D、y=lnx+
|
考点:基本不等式
专题:不等式的解法及应用
分析:A.由x>0,利用基本不等式的性质可得y=x+1+
≥2
=2,而等号不成立,因此不正确;
B.y=(x-1)2+2,当x=1时,y取得最小值2,正确;
C.y=
=x+1+
+5≥2
+5=9,因此最小值为9.
D.当0<x<1时,lnx<0,因此最小值不是2.
| 1 |
| x+1 |
(x+1)•
|
B.y=(x-1)2+2,当x=1时,y取得最小值2,正确;
C.y=
| x2+x+6(x+1)+4 |
| x+1 |
| 4 |
| x+1 |
(x+1)•
|
D.当0<x<1时,lnx<0,因此最小值不是2.
解答:
解:A.∵x>0,∴y=x+1+
≥2
=2,而等号不成立,因此y>2,故最小值不是2.
B.y=(x-1)2+2,当x=1时,y取得最小值2,正确;
C.y=
=x+1+
+5≥2
+5=9,当且仅当x=1时取等号,因此最小值为9,不是2.
D.当0<x<1时,lnx<0,因此最小值不是2.
综上可得:只有B正确.
故选:B.
| 1 |
| x+1 |
(x+1)•
|
B.y=(x-1)2+2,当x=1时,y取得最小值2,正确;
C.y=
| x2+x+6(x+1)+4 |
| x+1 |
| 4 |
| x+1 |
(x+1)•
|
D.当0<x<1时,lnx<0,因此最小值不是2.
综上可得:只有B正确.
故选:B.
点评:本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
(理数)使函数f(x)=2sin(2x+θ+
)是奇函数,且在[0,
]上是减函数的θ的一个值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某学校在“11•9”举行老师、学生消防知识比赛,报名的学生和教师的人数之比为6:1,学校决定按分层抽样的方法从报名的师生中抽取35人组队进行比赛,已知教师甲被抽到的概率为
,则报名的学生人数是 .
| 1 |
| 10 |
直线xtan
+y+2=0的倾斜角α是( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知a=(
)
,b=(
)
,c=log
,则a,b,c之间的大小关系为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
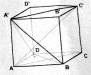 在正方体ABCD-A′B′C′D′中,求证:
在正方体ABCD-A′B′C′D′中,求证: