题目内容
a＞b＞0，求a2+
的最小值．
| 1 | ||
|
考点：基本不等式
专题：不等式的解法及应用
分析：两次利用基本不等式即可得出．
解答：
解：∵a＞b＞0，
∴a2+
≥a2+
=a2+
=a2+
+
≥3
=3，
当且仅当a=1=2b时取等号．
因此a2+
的最小值是3．
∴a2+
| 1 | ||
|
| 1 | ||
|
| 2 |
| a |
| 1 |
| a |
| 1 |
| a |
| 3 | a2•
| ||||
当且仅当a=1=2b时取等号．
因此a2+
| 1 | ||
|
点评：本题考查了基本不等式的性质，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
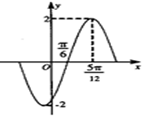已知函数f（x）=Msin（ωx+φ）（x∈R，M＞0，ω＞0，|φ|＜