题目内容
已知函数f（x）=Msin（ωx+φ）（x∈R，M＞0，ω＞0，|φ|＜| π |
| 2 |
（Ⅰ）求f（x）的解析式；
（Ⅱ）在锐角△ABC中，a，b，c分别是角A，B，C的对应边，且a=
| 7 |
| 3 |
3
| ||
| 2 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,余弦定理
专题：三角函数的图像与性质,解三角形
分析：（Ⅰ）由三角函数图象直接看出M和四分之一周期，求得周期后可求得ω，再由五点作图的第二点求得φ，则f（x）的解析式可求；
（Ⅱ）由f（A）=
求得交A，再利用三角形的面积公式求得bc的值，结合余弦定理与a=
求出b2+c2，则b+c=
=5．
（Ⅱ）由f（A）=
| 3 |
| 7 |
| b2+c2+2bc |
解答：
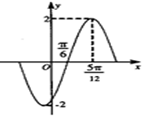
解：（Ⅰ）由图可得：M=2，
=
-
=
，
∴T=π，则ω=2．
由2×
+φ=0，得φ=-
．
∴f(x)=2sin(2x-
)；
（Ⅱ）∵f(A)=
，
∴2sin(2A-
)=
，sin(2A-
)=
，
∵0＜A＜
，
∴-
＜2A-
＜
，
∴2A-
=
⇒A=
，
在锐角△ABC中，∠A=
，
∴S△ABC=
bcsin
=
，
∴bc=6．
由余弦定理得：cosA=
=cos
=
，
整理得：b2+c2=13．
∴b+c=
=5．
| T |
| 4 |
| 5π |
| 12 |
| π |
| 6 |
| π |
| 4 |
∴T=π，则ω=2．
由2×
| π |
| 6 |
| π |
| 3 |
∴f(x)=2sin(2x-
| π |
| 3 |
（Ⅱ）∵f(A)=
| 3 |
∴2sin(2A-
| π |
| 3 |
| 3 |
| π |
| 3 |
| ||
| 2 |
∵0＜A＜
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴2A-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
在锐角△ABC中，∠A=
| π |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| π |
| 3 |
3
| ||
| 2 |
∴bc=6．
由余弦定理得：cosA=
| b2+c2-a2 |
| 2bc |
| π |
| 3 |
| 1 |
| 2 |
整理得：b2+c2=13．
∴b+c=
| b2+c2+2bc |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定函数解析式，考查了三角形的解法，注重考查三角函数化简和余弦定理的巧妙应用，是中档题．
练习册系列答案
相关题目