题目内容
8.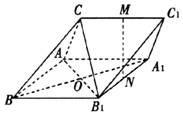 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.(I)证明:直线MN∥平面CAB1;
(II)BA=BC=BB1,CA=CB1,CA⊥CB1,∠ABB1=60°,求平面AB1C和平面A1B1C1所成的角(锐角)的余弦值.
分析 (Ⅰ)设AB1与A1B交于点O,连接CO,ON,说明O是AB1的中点,证明四边形CMNO是平行四边形,推出MN∥CO.然后证明直线MN∥平面CAB1.
(Ⅱ)以O为坐标原点,OB,OB1,OC所在直线分别为x,y,z轴建立如图空间直角坐标系O-xyz,设OB=1,求出相关点的坐标,求出平面AB1C的一个法向量;平面A1B1C1的一个法向量,利用空间向量的数量积求解平面AB1C和平面A1B1C1所成的角(锐角)的余弦值.
解答 (本小题满分12分)
证明:(Ⅰ)设AB1与A1B交于点O,连接CO,ON,
因为四边形ABB1A1是平行四边形,所以是O是AB1的中点,
N是A1B1的中点,所以$ON∥A{A_1},ON=\frac{1}{2}A{A_1}$.
又因为M是CC1的中点,所以$CM∥A{A_1},CM=\frac{1}{2}A{A_1}$.
所以CM$\stackrel{∥}{=}$ON,所以四边形CMNO是平行四边形,
所以MN∥CO.
又因为MN?平面CAB1,CO?平面CAB1,
所以直线MN∥平面CAB1.…(5分)
(Ⅱ)因为AB=BB1,所以平行四边形ABB1A1是菱形,所以BA1⊥AB1.
又因为CA=CB1,所以CO⊥AB1.
又CA⊥CB1,且O是AB1的中点,所以AO=CO.又因为BA=BC,所以△BOC≌△BOA,
所以∠BOC=∠BOA,故OC⊥OB,从而OA,OB,OC两两垂直.
以O为坐标原点,OB,OB1,OC所在直线分别为x,y,z轴建立如图空间直角坐标系O-xyz,设OB=1,因为∠ABB1=60°,BA=BB1, 所
所
以△ABB1是等边三角形,所以$A(0,-\frac{{\sqrt{3}}}{3},0),{B_1}(0,\frac{{\sqrt{3}}}{3},0),C(0,0,\frac{{\sqrt{3}}}{3})$,B(1,0,0),$\overrightarrow{{A_1}{C_1}}=\overrightarrow{AC}=(0,\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3})$,$\overrightarrow{{C_1}{B_1}}=\overrightarrow{CB}=(1,0,-\frac{{\sqrt{3}}}{3})$.
因为OA,OB,OC两两垂直,所以OB⊥平面AB1C,
所以$\overrightarrow{OB}=(1,0,0)$是平面AB1C的一个法向量;
设$\overrightarrow{m}$=(x,y,z)是平面A1B1C1的一个法向量,则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{A}_{1}{C}_{1}}=0}\\{\overrightarrow{m}•\overrightarrow{{C}_{1}{B}_{1}}=0}\end{array}\right.$,即$\left\{{\begin{array}{l}{\frac{{\sqrt{3}}}{3}y+\frac{{\sqrt{3}}}{3}z=0}\\{x-\frac{{\sqrt{3}}}{3}z=0}\end{array}}\right.$,令$z=\sqrt{3}$,得$x=1,y=-\sqrt{3}$,所以$\overrightarrow{m}$=$(1,-\sqrt{3},\sqrt{3})$,
所以$cos<\overrightarrow{m},\overrightarrow{OB}>$=$\frac{\overrightarrow{m}•\overrightarrow{OB}}{|\overrightarrow{m}||\overrightarrow{OB}|}$=$\frac{1}{\sqrt{7}}$=$\frac{\sqrt{7}}{7}$.
所以平面AB1C和平面A1B1C1所成的角(锐角)的余弦值为$\frac{{\sqrt{7}}}{7}$.…(12分)
点评 本题考查平面与平面所成角的求法,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.


| A. | 6+4$\sqrt{2}$ | B. | 4+4$\sqrt{2}$ | C. | 2 | D. | 8 |
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
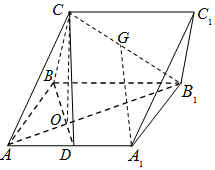 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.