题目内容
12.已知f(x)=$\left\{\begin{array}{l}{ln(1-x),x<0}\\{{x}^{2}-ax,x≥0}\end{array}\right.$,且g(x)=f(x)+$\frac{x}{2}$有三个零点,则实数a的取值范围为($\frac{1}{2}$,+∞).分析 由题意画出图形,可知y=-$\frac{x}{2}$与y=ln(1-x)(x<0)一定有一交点;然后分a≤0和a>0分类分析,当a≤0时,函数y=f(x)的图象与y=-$\frac{x}{2}$的图象有两个不同交点,不满足题意;当a>0时,联立$\left\{\begin{array}{l}{y=-\frac{x}{2}}\\{y={x}^{2}-ax}\end{array}\right.$,得2x2-(2a-1)x=0,可得方程2x2-(2a-1)x=0有一0根一正根,由此列式求得a的范围.
解答 解:函数g(x)=f(x)+$\frac{x}{2}$有三个零点,即方程f(x)+$\frac{x}{2}$=0有三个根,
也就是函数y=f(x)的图象与y=-$\frac{x}{2}$的图象有三个不同交点.
如图:
y=-$\frac{x}{2}$与y=ln(1-x)(x<0)一定有一交点;
当a≤0时,y=x2-ax(x≥0)的图象是图中虚线部分,
∴函数y=f(x)的图象与y=-$\frac{x}{2}$的图象有两个不同交点,不满足题意;
当a>0时,联立$\left\{\begin{array}{l}{y=-\frac{x}{2}}\\{y={x}^{2}-ax}\end{array}\right.$,得2x2-(2a-1)x=0.
若函数y=f(x)的图象与y=-$\frac{x}{2}$的图象有三个不同交点,则方程2x2-(2a-1)x=0有一0根一正根,
则$\frac{2a-1}{2}>0$,即a>$\frac{1}{2}$.
∴实数a的取值范围为:($\frac{1}{2}$,+∞).
故答案为:($\frac{1}{2}$,+∞).
点评 本题考查根的存在性与根的个数判断,考查数学转化思想方法和数形结合的解题思想方法,是中档题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | $\frac{1}{5}$ | B. | -$\frac{7}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{7}{5}$ |
| A. | 命题“?x0∈R,sinx0>1”的否定是“?x∈R,sinx>1” | |
| B. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” | |
| C. | 在△ABC中,A>B是sinA>sinB的充分不必要条件 | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
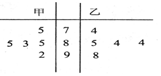 如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )| A. | x1<x2,y1<y2 | B. | x1<x2,y1>y2 | C. | x1>x2,y1>y2 | D. | x1>x2,y1<y2 |
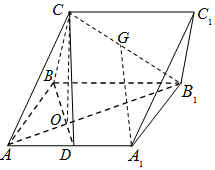 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.