题目内容
已知圆C的半径为3,圆心C在直线2x+y=0上且在x轴的下方,x轴被圆C截得的弦长BD为2
.
(1)求圆C的方程;
(2)若圆E与圆C关于直线2x-4y+5=0对称,P(x,y)为圆E上的动点,求
的取值范围.
| 5 |
(1)求圆C的方程;
(2)若圆E与圆C关于直线2x-4y+5=0对称,P(x,y)为圆E上的动点,求
| (x-1)2+(y+2)2 |
考点:直线与圆相交的性质
专题:综合题,直线与圆
分析:(1)由题意可设方程为(x-a)2+(y+2a)2=9,由条件可得a=1,进而可得方程;
(2)设圆心E(m,n),由对称关系可得m=-2,n=4,半径为3,
表示圆E上的点与(1,-2)的距离,即可求出
的取值范围..
(2)设圆心E(m,n),由对称关系可得m=-2,n=4,半径为3,
| (x-1)2+(y+2)2 |
| (x-1)2+(y+2)2 |
解答:
解:(1)由题意设圆心坐标(a,-2a)---(1分),则圆方程为(x-a)2+(y+2a)2=9----(2分)
作CA⊥x轴于点A,在Rt△ABC中,CB=3,AB=
,∴CA=2,-------(4分)
所以|-2a|=2,解得a=±1-----------(5分)
又因为点C在x轴的下方,所以a=1,即C(1,-2)-----------(6分)
所以圆方程为:(x-1)2+(y+2)2=9------------(7分)
(2)设圆心E(m,n),由题意可知点E与点C是关于直线2x-4y+5=0对称,
所以有
--------(9分)可解得m=-2,n=4------------(11分)
所以点E(-2,4)且圆E的半径为3--------(12分)
所以圆E的方程为(x+2)2+(y-4)2=9,
表示圆E上的点与(1,-2)的距离.
因为(1,-2)与点E(-2,4)的距离为
=3
,
所以
的取值范围为[3
-3,3
+3].
作CA⊥x轴于点A,在Rt△ABC中,CB=3,AB=
| 5 |
所以|-2a|=2,解得a=±1-----------(5分)
又因为点C在x轴的下方,所以a=1,即C(1,-2)-----------(6分)
所以圆方程为:(x-1)2+(y+2)2=9------------(7分)
(2)设圆心E(m,n),由题意可知点E与点C是关于直线2x-4y+5=0对称,
所以有
|
所以点E(-2,4)且圆E的半径为3--------(12分)
所以圆E的方程为(x+2)2+(y-4)2=9,
| (x-1)2+(y+2)2 |
因为(1,-2)与点E(-2,4)的距离为
| (1+2)2+(-2-4)2 |
| 5 |
所以
| (x-1)2+(y+2)2 |
| 5 |
| 5 |
点评:本题考查直线和圆的位置关系,以及对称问题,考查学生分析解决问题的能力,属中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
在△ABC中,如果AB=5,AC=3,BC=4,那么角
•
等于( )
| AB |
| AC |
| A、9 | B、12 | C、15 | D、20 |
已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若asinA-csinC=(a-b)sinB,则角C为( )
| A、60° | B、30° |
| C、120° | D、150° |
方程4x-2x+1+4m=0只有一个实数解,则实数m的取值范围是( )
| A、{m|m≤0} | ||
B、{m|0<m<
| ||
C、{m|m>
| ||
D、{m|m≤0或m=
|
方程|sinx|=kx(k>0)有且仅有两个不同的非零实数解θ,Φ(θ>Φ),则以下有关两根关系的结论正确的是( )
| A、sinΦ=Φcosθ |
| B、sinΦ=-Φcosθ |
| C、cosΦ=θsin |
| D、sinθ=-θsinΦ |
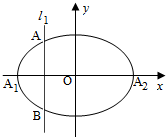 如图,椭圆Γ:
如图,椭圆Γ: