题目内容

已知x、y、z均为正数．求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：利用基本不等式，即可证明结论．
解答： 证明：因为x、y、z都是正数，所以
x
yz
+
y
zx
=
1
z
×2
x
y
×
y
x
≥
2
z
．…（3分）
同理可得
y
zx
+
z
xy
≥
2
x
，
z
xy
+
x
yz
≥
2
y
．
将上述三个不等式两边分别相加，并除以2，得
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．…（10分）
点评：本题考查不等式的证明，考查基本不等式，难度一般．
练习册系列答案
相关题目
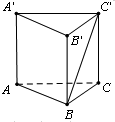如图所示，在底面为正三角形的三棱柱ABC-A1B1C1中，若AA1⊥平面ABC，AB=
2
BB，则AB1与C1B所成角的大小为（　　）
A、60°B、45°
C、90°D、120°
阅读下面材料：
由曲线y=sinx，x∈[0，π]，直线x=0，x=π及x轴围成的封闭图形的面积为2；
由曲线y=sin2x，x∈[0，
π
2
]，直线x=0，x=
π
2
及x轴围成的封闭图形的面积为1；
由曲线y=sin3x，x∈[0，
π
3
]，直线x=0，x=
π
3
及x轴围成的封闭图形的面积为
2
3
；…
据此猜想：由曲线y=Asin(ωx+φ)，(A＞0，ω＞0)，x∈[0，
π
ω
]，直线x=0，x=
π
ω
及x轴围成的封
闭图形的面积为
 
．
已知椭圆C的中心在原点O，焦点在x轴上，椭圆的两焦点与椭圆短轴的一个端点构成等边三角形，右焦点到右顶点的距离为1．
（1）求椭圆C的标准方程；
（2）是否存在与椭圆C交于A，B两点的直线l：y=kx+m（k∈R），使得|
OA
+2
OB
|=|
OA
-2
OB
|成立？若存在，求出实数m的取值范围；若不存在，请说明理由．
已知曲线E：
x2
m
+
y2
m-1
=1，
（1）若曲线E为双曲线，求实数m的取值范围；
（2）已知m=4，A（-1，0）和曲线C：（x-1）2+y2=16，点P是曲线C上任意一点，线段PA的垂直平分线为l，试判断l与曲线E的位置关系，并证明你的结论．
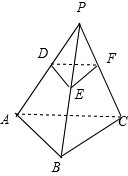如图，已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且
PD
PA
=
PE
PB
=
PF
PC
求证平面DEF∥平面ABC．
设角A，B，C为△ABC三个内角，已知cos（B+C）+sin2
A
2
=
5
4
．
（1）求角A的大小；
（2）若
AB
•
AC
=-1，求BC边上的高AD长的最大值．
已知圆C的半径为3，圆心C在直线2x+y=0上且在x轴的下方，x轴被圆C截得的弦长BD为2
5
．
（1）求圆C的方程；
（2）若圆E与圆C关于直线2x-4y+5=0对称，P（x，y）为圆E上的动点，求
(x-1)2+(y+2)2
的取值范围．
已知命题p：关于x的方程x2+ax+4-a2=0有一正一负两根，命题q：函数y=（a-1）x+1为增函数，若“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网