Question

方程|sinx|=kx（k＞0）有且仅有两个不同的非零实数解θ，Φ（θ＞Φ），则以下有关两根关系的结论正确的是（　　）

• A、sinΦ=Φcosθ
• B、sinΦ=-Φcosθ
• C、cosΦ=θsin
• D、sinθ=-θsinΦ

Answer 1

考点：函数的零点与方程根的关系

专题：计算题,作图题,函数的性质及应用,导数的综合应用

分析：由题意，函数y=|sinx|与y=kx（k＞0）有且仅有两个不同的交点，作图可知y=kx与y=-sinx在[π，2π]上相切；从而求解．

解答： 解：∵方程|sinx|=kx（k＞0）有且仅有两个不同的非零实数解θ，Φ（θ＞Φ），
∴函数y=|sinx|与y=kx（k＞0）有且仅有两个不同的交点，如下图，

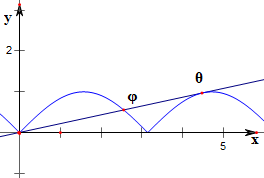
则y=kx与y=-sinx在[π，2π]上相切；
故y′=-cosx，故y′=-cosθ；
由联立方程得，

y=sinx y=-cosθx

，
解得，sinφ=-φcosθ；
故选B．

点评：本题考查了函数的图象的应用及导数的综合应用，属于基础题．