题目内容
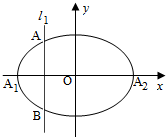 如图,椭圆Γ:
如图,椭圆Γ:| x2 |
| 4 |
| y2 |
| 3 |
椭圆Γ的左、右顶点,l1与椭圆Γ相交于A,B两点(点A在第二象限).
(Ⅰ)求直线AA1与直线A2B交点M的轨迹方程;
(Ⅱ)设动直线l2:x=x2(-2<x<2,x1≠x2)与椭圆Γ相交于C,D两点,△OAB与△OCD的面积相等.证明:|OA|2+|OD|2为定值.
考点:轨迹方程,直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出直线A1A的方程、直线A2B的方程,联立,结合点A(x1,y1)在椭圆Γ上,即可求直线AA1与直线A2B交点M的轨迹方程;
(Ⅱ)设C(x2,y2),由△OAB与△OCD的面积相等,得|x1||y1|=|x2||y2|⇒x12•y12=x22•y22,结合点A,C均在椭圆上,即可证明结论.
(Ⅱ)设C(x2,y2),由△OAB与△OCD的面积相等,得|x1||y1|=|x2||y2|⇒x12•y12=x22•y22,结合点A,C均在椭圆上,即可证明结论.
解答:
(Ⅰ)解:设A(x1,y1),B(x1,-y1),又A1(-2,0),A2(2,0),
则直线A1A的方程为:y=
(x+2)①
直线A2B的方程为:y=
(x-2)②
由①②得:y2=
(x2-4)③
由点A(x1,y1)在椭圆Γ上,故可得
+
=1,
∴y12=3(1-
),代入③得:
-
=1(x<-2,y<0)
(Ⅱ)证明:设C(x2,y2),
由△OAB与△OCD的面积相等,得|x1||y1|=|x2||y2|⇒x12•y12=x22•y22,
因为点A,C均在椭圆上,
∴3x12(1-
)=3x22(1-
)
由x1≠x2,所以x12+x22=4.
∴y12+y22=3,
∴|OA|2+|OD|2=7为定值
则直线A1A的方程为:y=
| y1 |
| x1+2 |
直线A2B的方程为:y=
| -y1 |
| x1-2 |
由①②得:y2=
| -y12 |
| x12-4 |
由点A(x1,y1)在椭圆Γ上,故可得
| x12 |
| 4 |
| y12 |
| 3 |
∴y12=3(1-
| x12 |
| 4 |
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:设C(x2,y2),
由△OAB与△OCD的面积相等,得|x1||y1|=|x2||y2|⇒x12•y12=x22•y22,
因为点A,C均在椭圆上,
∴3x12(1-
| x12 |
| 4 |
| x22 |
| 4 |
由x1≠x2,所以x12+x22=4.
∴y12+y22=3,
∴|OA|2+|OD|2=7为定值
点评:本题考查椭圆方程,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
sin21°+sin22°+sin23°+sin288°+sin289°+sin290°=( )
| A、45 | ||||
B、45
| ||||
C、
| ||||
D、
|
若2x=8Y+1且9y=3x-9,则x+y的值是( )
| A、18 | B、24 | C、21 | D、27 |
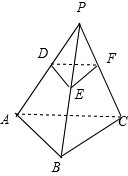 如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且
如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且