题目内容
15.(x-$\frac{2}{\sqrt{x}}$)5的展开式中x2的系数为( )| A. | 40 | B. | 80 | C. | -32 | D. | -80 |
分析 Tr+1=${C}_{5}^{r}{x}^{5-r}(-\frac{2}{\sqrt{x}})^{r}$=(-2)r${C}_{5}^{r}$x${\;}^{5-\frac{3}{2}r}$,令5-$\frac{3}{2}r=2$,解得r=2,由此能求出(x-$\frac{2}{\sqrt{x}}$)5的展开式中x2的系数.
解答 解:∵(x-$\frac{2}{\sqrt{x}}$)5,
∴Tr+1=${C}_{5}^{r}{x}^{5-r}(-\frac{2}{\sqrt{x}})^{r}$=(-2)r${C}_{5}^{r}$x${\;}^{5-\frac{3}{2}r}$,
令5-$\frac{3}{2}r=2$,解得r=2,
∴(x-$\frac{2}{\sqrt{x}}$)5的展开式中x2的系数为:(-2)2${C}_{5}^{2}$=40.
故选:A.
点评 本题考查二项展开式中含x2的项的系数的求法,考查二项式定理、通项公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若x,y且x+y>2,则$\frac{1+y}{x}$和$\frac{1+x}{y}$的值满足( )
| A. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都大于2 | B. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都小于2 | ||
| C. | $\frac{1+y}{x}$和$\frac{1+x}{y}$中至少有一个小于2 | D. | 以上说法都不对 |
7.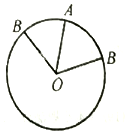 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
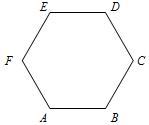 如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.
如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.