题目内容
已知集合A={y|y=x2-
x+1,x∈[
,2]},B={x|x+m2≥1},p:x∈A,q:x∈B,且p是q的充分不必要条件.
(1)当m=
时,求集合A∩B;
(2)求实数m的取值范围.
| 3 |
| 2 |
| 3 |
| 4 |
(1)当m=
| 1 |
| 4 |
(2)求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:(1)利用不等式和函数的性质求出集合A,B,利用集合的基本运算即可得到结论.
(2)根据p是q的充分不必要条件,建立条件关系即可得到结论.
(2)根据p是q的充分不必要条件,建立条件关系即可得到结论.
解答:
解:(1)y=x2-
x+1=(x-
)x2+
,x∈[
,2]},
∴当x=
时,函数取得最小值为
,
当x=2时,函数取得最大值为y=2,
∴A=[
,2].
当m=
时,B={x|x≥
},
则集合A∩B=[
,2].
(2)B={x|x+m2≥1}=B={x|x≥1-m2},
∵p是q的充分不必要条件.
∴1-m2≤
,
即m2≥
,
解得m≥
或m≤-
,
即m的取值范围是{m|m≥
或m≤-
}.
| 3 |
| 2 |
| 3 |
| 4 |
| 7 |
| 16 |
| 3 |
| 4 |
∴当x=
| 3 |
| 4 |
| 7 |
| 16 |
当x=2时,函数取得最大值为y=2,
∴A=[
| 7 |
| 16 |
当m=
| 1 |
| 4 |
| 15 |
| 16 |
则集合A∩B=[
| 16 |
| 15 |
(2)B={x|x+m2≥1}=B={x|x≥1-m2},
∵p是q的充分不必要条件.
∴1-m2≤
| 7 |
| 16 |
即m2≥
| 9 |
| 16 |
解得m≥
| 3 |
| 4 |
| 3 |
| 4 |
即m的取值范围是{m|m≥
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题主要考查集合的基本运算,以及充分条件和必要条件的应用,考查学生的运算能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
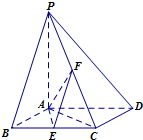 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.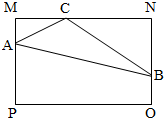 如图,已知四边形MNOP是一个矩形,MN=
如图,已知四边形MNOP是一个矩形,MN=