题目内容
已知函数f(x)的导数为f′(x),且满足关系式f(x)=2x3+x2f'(1)+lnx,则f′(2)的值等于( )
A、-
| ||
B、
| ||
| C、-7 | ||
| D、7 |
考点:导数的加法与减法法则
专题:计算题,导数的概念及应用
分析:由f′(x)=6x2+2xf′(1)+
可得f′(1)=6+2f′(1)+1,从而求出f′(1),代入求f′(2).
| 1 |
| x |
解答:
解:由题意,
f′(x)=6x2+2xf′(1)+
,
则f′(1)=6+2f′(1)+1,
则f′(1)=-7;
故f′(2)=24+2×2×(-7)+
=-
,
故选A.
f′(x)=6x2+2xf′(1)+
| 1 |
| x |
则f′(1)=6+2f′(1)+1,
则f′(1)=-7;
故f′(2)=24+2×2×(-7)+
| 1 |
| 2 |
=-
| 7 |
| 2 |
故选A.
点评:本题考查了导数的运算,属于基础题.

练习册系列答案
相关题目
函数f(x)=
在点P(2,f(2))处切线方程是( )
| ex |
| x |
A、y=
| ||
B、y=e2x-
| ||
C、y=
| ||
D、y=3e2x-
|
下列函数中,既是偶函数又在区间(-∞,0)上单调递减的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
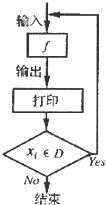 对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下: