题目内容
下列函数中,既是偶函数又在区间(-∞,0)上单调递减的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性的性质分别进行判断即可.
解答:
解:A.f(x)=
为偶函数,在区间(-∞,0)上单调递增,不满足条件.
B.f(x)=x2+1为偶函数,在区间(-∞,0)上单调递减,满足条件.
C.f(x)=x3为奇函数,在区间(-∞,0)上单调递增,不满足条件.
D.f(x)=2-x为非奇非偶函数,在区间(-∞,0)上单调递减,不满足条件.
故选:B
| 1 |
| x2 |
B.f(x)=x2+1为偶函数,在区间(-∞,0)上单调递减,满足条件.
C.f(x)=x3为奇函数,在区间(-∞,0)上单调递增,不满足条件.
D.f(x)=2-x为非奇非偶函数,在区间(-∞,0)上单调递减,不满足条件.
故选:B
点评:本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性的性质.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知函数f(x)的导数为f′(x),且满足关系式f(x)=2x3+x2f'(1)+lnx,则f′(2)的值等于( )
A、-
| ||
B、
| ||
| C、-7 | ||
| D、7 |
在△ABC中,若a=6,b=12,A=60°,则此三角形解的情况( )
| A、一解 | B、两解 |
| C、无解 | D、解的个数不能确定 |
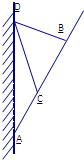 某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°
某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°