题目内容
设常数a>0,则
(1)函数f(x)=
的值域为 ;
(2)若函数f(x)=
为奇函数,则a= .
(1)函数f(x)=
| 2x+a |
| 2x-a |
(2)若函数f(x)=
| 2x+a |
| 2x-a |
考点:函数奇偶性的性质,函数的值域
专题:函数的性质及应用
分析:本题(1)先将函数式变形为部分分式,再利用分式不为0的特征得到函数的值域;(2)利用函数奇偶性的定义,得到关于x的恒等式,研究恒等式,得到本题结论.
解答:
解:(1)∵a>0,
∴函数f(x)=
=1+
≠1,
∴函数f(x)=
的值域为(-∞,1)∪(1,+∞).
(2)∵函数f(x)=
为奇函数,
∴f(-x)=-f(x).
∴
=-
,
∴2(a2-1)2x=0,
∴a2=1,
∵常数a>0,
∴a=1.
故答案为:(1)(-∞,1)∪(1,+∞);(2)1.
∴函数f(x)=
| 2x+a |
| 2x-a |
| 2a |
| 2x-a |
∴函数f(x)=
| 2x+a |
| 2x-a |
(2)∵函数f(x)=
| 2x+a |
| 2x-a |
∴f(-x)=-f(x).
∴
| 2-x+a |
| 2-x-a |
| 2x+a |
| 2x-a |
∴2(a2-1)2x=0,
∴a2=1,
∵常数a>0,
∴a=1.
故答案为:(1)(-∞,1)∪(1,+∞);(2)1.
点评:本题考查了函数的值域和函数奇偶性的应用,本题难度不大,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则此几何体的体积为( )
如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则此几何体的体积为( )| A、6 | B、9 | C、12 | D、18 |
已知函数f(x)的导数为f′(x),且满足关系式f(x)=2x3+x2f'(1)+lnx,则f′(2)的值等于( )
A、-
| ||
B、
| ||
| C、-7 | ||
| D、7 |
函数y=f(x)是R上的偶函数,且在(-∞,0]上是增函数,若f(a)≤f(2),则实数a的取值范围是( )
| A、(-∞,2] |
| B、[-2,+∞) |
| C、[-2,2] |
| D、(-∞,-2]∪[2,+∞) |
 已知函数f(x)=
已知函数f(x)=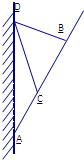 某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°
某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°