题目内容
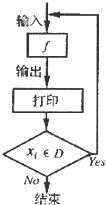 对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:①输入数据x0∈D,经数列发生器输出x1=f(x0);
②若x1∉D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.现定义f(x)=
| 4x-2 |
| x+1 |
(1)若输出x0=
| 49 |
| 65 |
(2)若要数列发生器产生一个无穷的常数数列,试求输出的初始数据x0的值;
(3)是否存在 x0,在输入数据x0时,该数列发生器产生一个各项均为负数的无穷数列?若存在,求出x0的值;若不存在,请说明理由.
考点:程序框图
专题:压轴题
分析:(1)利用f(x)=
,x0=
及工作原理,注意函数的定义域,直接可求得数列{xn}的只有三项;
(2)要数列发生器产生一个无穷的常数列,则有f(x)=
,从而求出相应的初始数据x0的值;
(3)设 x0<0,(n∈N*),验证可知同时x1,x2,x3使为负数的x0不存在,故所求的x0不存在.
| 4x-2 |
| x+1 |
| 49 |
| 65 |
(2)要数列发生器产生一个无穷的常数列,则有f(x)=
| 4x-2 |
| x+1 |
(3)设 x0<0,(n∈N*),验证可知同时x1,x2,x3使为负数的x0不存在,故所求的x0不存在.
解答:
解:(1)因为f(x)的定义域D=(-∞,-1)∪(-1,+∞),所以数列{xn}只有三项x1=
,x2=
,x3=-1.
(2)因为f(x)=
,即x2-3x+2=0,所以x=1或x=2,即x0=1或x0=2时,xn+1=
=xn,
故当x0=1时,xn=1;当x0=2时,xn=2(n∈N*).
(3)设 x0<0,(n∈N*)
由x1=
<0,得-1<x0<
;
由x2=
<0,得
<x0<
;
由x3=
<0,得
<x0<
.
∵
<
∴同时x1,x2,x3使为负数的x0不存在,故所求的x0不存在.
| 11 |
| 19 |
| 1 |
| 5 |
(2)因为f(x)=
| 4x-2 |
| x+1 |
| 4xn-2 |
| xn+1 |
故当x0=1时,xn=1;当x0=2时,xn=2(n∈N*).
(3)设 x0<0,(n∈N*)
由x1=
| 4x0-2 |
| x0+1 |
| 1 |
| 2 |
由x2=
| 14x0-10 |
| 5x0-1 |
| 1 |
| 5 |
| 5 |
| 7 |
由x3=
| 2(23x0-19) |
| 19x0-11 |
| 11 |
| 19 |
| 19 |
| 23 |
∵
| 1 |
| 2 |
| 11 |
| 19 |
∴同时x1,x2,x3使为负数的x0不存在,故所求的x0不存在.
点评:本题是数列与算法的简单结合,应搞清算法原理,将问题等价转化,有一定的难度.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知函数f(x)的导数为f′(x),且满足关系式f(x)=2x3+x2f'(1)+lnx,则f′(2)的值等于( )
A、-
| ||
B、
| ||
| C、-7 | ||
| D、7 |
下列不等关系中,正确的是( )
A、(
| ||||||||
B、(
| ||||||||
C、1<(
| ||||||||
D、(
|
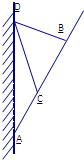 某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°
某固定在墙上的广告金属支架如图所示,根据要求,AB至少长3米,C为AB的中点,B到D的距离比CD的长小0.5米,∠BCD=60°