题目内容
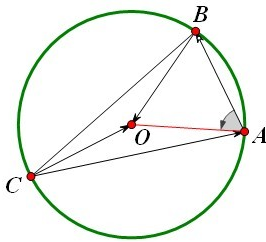
已知△ABC内接于圆O（圆心是三边垂直平分线的交点），若
•
=2
•
，且|AB|=3，|CA|=6，则cosA的值是（ ）
| CO |
| AB |
| BO |
| CA |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题设条件，利用平面向量的数量积公式，得到3r•cos∠OAB+4r•cos∠OAC=18•cos∠A，再由余弦定理能求出cosA的值．
解答：
解：∵
•
=2
•
，
∴（
+
）•
=2（
+
）•
，
∴
•
+
•
=2
•
+2
•
，
∴
•
-2
•
=2
•
-
•
，
∴
•
+2
•
=2
•
+
•
，
∴
•
+2
•
=3
•
，
设圆半径为r，
则r•3•cos∠OAB+2•r•6•cos∠OAC=3•3•6•cos∠A，
3r•cos∠OAB+4r•cos∠OAC=18•cos∠A，①
分别在△OAB，△OAC中使用余弦定理，来表示出cos∠OAB与cos∠OAC，
∵OB2=AO2+AB2-2AO•AB•cos∠OAB，
即：r2 =r2+32-2r•3•cos∠OAB，
∴cos∠OAB=
，
同理：cos∠OAC=
，
把此两式代入①中，解得：cosA=
．
故选：A．
解：∵| CO |
| AB |
| BO |
| CA |
∴（
| CA |
| AO |
| AB |
| BA |
| AO |
| CA |
∴
| CA |
| AB |
| AO |
| AB |
| BA |
| CA |
| AO |
| CA |
∴
| AO |
| AB |
| AO |
| CA |
| AB |
| AC |
| CA |
| AB |
∴
| AO |
| AB |
| AO |
| AC |
| AB |
| AC |
| AC |
| AB |
∴
| AO |
| AB |
| AO |
| AC |
| AB |
| AC |
设圆半径为r，
则r•3•cos∠OAB+2•r•6•cos∠OAC=3•3•6•cos∠A，
3r•cos∠OAB+4r•cos∠OAC=18•cos∠A，①
分别在△OAB，△OAC中使用余弦定理，来表示出cos∠OAB与cos∠OAC，
∵OB2=AO2+AB2-2AO•AB•cos∠OAB，
即：r2 =r2+32-2r•3•cos∠OAB，
∴cos∠OAB=
| 3 |
| 2r |
同理：cos∠OAC=
| 3 |
| r |
把此两式代入①中，解得：cosA=
| 3 |
| 4 |
故选：A．
点评：本题考查平面向量的数量积的应用，是中档题，解题时要注意余弦定理的合理运用．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
“x＜-2”是“x≤0”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
在（-π，2π）内与
终边相同的角有（ ）个．
| 3π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
已知方程组
对此方程组的每一组正实数解（x，y，z，u），其中z≥y，都存在正实数M，且满足M≤
，则M的最大值是（ ）
|
| z |
| y |
| A、1 | ||
B、3+2
| ||
C、6+4
| ||
D、3-2
|
利用秦九韶算法计算多项式f（x）=3x6+4x5+5x4+6x3+7x2+8x+1当x=4的值的时候需要做乘法和加法的次数分别为（ ）??
| A、6?6 | B、5?6 |
| C、5?5 | D、6?5 |
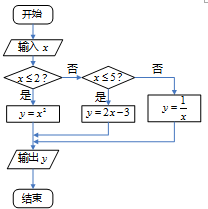给出了一个程序框图，其作用是输入x的值，输出相应的y的值，
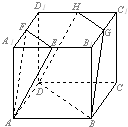如图，E，F，G，H分别为正方体AC1的棱A1B1，A1D1，B1C1，D1C1的中点，
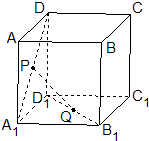正方体ABCD-A1B1C1D1的棱长为1，P、Q分别是正方形AA1D1D和A1B1C1D1的中心．