题目内容
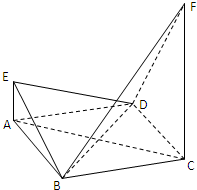 已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.
已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.(1)求证:平面EBD⊥平面FBD;
(2)求直线AB与平面EAD所成角的正弦值;
(3)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
考点:用空间向量求直线与平面的夹角,组合几何体的面积、体积问题,平面与平面垂直的判定,直线与平面所成的角
专题:计算题,证明题,空间位置关系与距离,空间角,空间向量及应用
分析:(1)连结EO与FO,通过证明EO⊥平面FBD,然后证明平面EBD⊥平面FBD;
(2)以O为坐标原点,建立空间直角坐标系如图,设平面AED的法向量为:
=(x,y,z),通过
,利用法向量直接求出直线AB与平面EAD所成角的正弦值;
(3)四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积,转化为两个四棱锥的体积减去两个三棱锥的体积.
(2)以O为坐标原点,建立空间直角坐标系如图,设平面AED的法向量为:
| n |
|
(3)四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积,转化为两个四棱锥的体积减去两个三棱锥的体积.
解答:
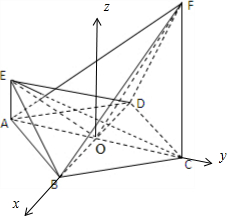
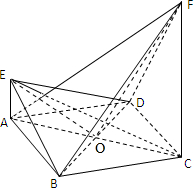
解:(1)证明:连结EO与FO,∵四边形ABCD是菱形,其对角线AC=4,BD=2,∴AO=2,OC=2,OD=0B=1,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.tan∠EOA=tan∠OFC,∴∠EOA+∠FOC=90°∴EO⊥OF.
△EAB≌△EAD,∴EA=ED,△BED是等腰三角形.∴EO⊥BD,∵BD∩OF=O,∴EO⊥平面FBD,EO?平面BDE,∴平面EBD⊥平面FBD.
(2)以O为坐标原点,建立空间直角坐标系如图,则A(0,-2,0),B(1,0,0),E(0,-2,1),D(-1,0,0),
=(0,0,1),
=(-1,2,0).
设平面AED的法向量为:
=(x,y,z),则
,即
,
=(2,1,0),
=(1,2,0).
∴直线AB与平面EAD所成角的正弦值为:sinθ=|
|=
=
.
(3)四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积
V=VE-ABCD+VF-ABCD-VE-ABD-VF-BCD
=
×
×4×2×1+
×
×4×2×4-
×
×
×2×4-
×
×
×4×2×4
=
.


|
△EAB≌△EAD,∴EA=ED,△BED是等腰三角形.∴EO⊥BD,∵BD∩OF=O,∴EO⊥平面FBD,EO?平面BDE,∴平面EBD⊥平面FBD.
(2)以O为坐标原点,建立空间直角坐标系如图,则A(0,-2,0),B(1,0,0),E(0,-2,1),D(-1,0,0),
| AE |
| AD |
设平面AED的法向量为:
| n |
|
|
| n |
| AB |
∴直线AB与平面EAD所成角的正弦值为:sinθ=|
| ||||
|
|
| 4 | ||||
|
| 4 |
| 5 |
(3)四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积
V=VE-ABCD+VF-ABCD-VE-ABD-VF-BCD
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 10 |
| 3 |
点评:本题考查空间位置关系,二面角平面角的作法以及空间几何体的体积计算等知识.考查利用综合法或向量法解决立体几何问题的能力.

练习册系列答案
相关题目
利用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=4的值的时候需要做乘法和加法的次数分别为( )??
| A、6?6 | B、5?6 |
| C、5?5 | D、6?5 |
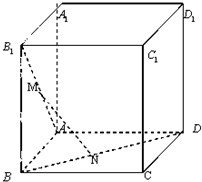 如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<
如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t< 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.