题目内容
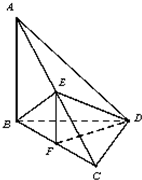 如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.
如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.(1)求证:CD⊥平面ABD;
(2)若CD=3,AC=10,求点C到平面DEF的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:(1)通过证明CD垂直平面ABD内的两条相交直线AB、AD,利用直线与平面垂直的判定定理即可证明CD⊥平面ABD;
(2)结合CD=3,AC=10,利用等体积法,即可求点C到平面DEF的距离.
(2)结合CD=3,AC=10,利用等体积法,即可求点C到平面DEF的距离.
解答:
(1)解:∵△BEC为正三角形,F为BC中点,
∴EF⊥BC,∵EF∥AB,∴AB⊥BC,
又∵AB⊥BD,∴AB⊥平面BCD …(3分)
∴AB⊥CD,又∵AD⊥CD,AB∩AD=A,
∴CD⊥平面ABD …(6分)
(2)设点C到平面DEF的距离为h,
∵AC=10,BE=BC=5,∴AB=2EF=5
,
在Rt△BDC中,∵F为BC中点,∴DF=
BC=
,∴S△EFD=
DF•EF=
∴VC-EFD=
S△EFD•h=
…(8分)
∵CD=3,BC=5,BD=4,∴S△DFC=
S△DBC=3.
∴VE-CFD=
S△CFD•EF=
…(10分)
VC-EFD=VE-CFD∴h=
∴点C到平面DEF的距离为
.…(12分)
∴EF⊥BC,∵EF∥AB,∴AB⊥BC,
又∵AB⊥BD,∴AB⊥平面BCD …(3分)
∴AB⊥CD,又∵AD⊥CD,AB∩AD=A,
∴CD⊥平面ABD …(6分)
(2)设点C到平面DEF的距离为h,
∵AC=10,BE=BC=5,∴AB=2EF=5
| 3 |
在Rt△BDC中,∵F为BC中点,∴DF=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
25
| ||
| 8 |
∴VC-EFD=
| 1 |
| 3 |
25
| ||
| 24 |
∵CD=3,BC=5,BD=4,∴S△DFC=
| 1 |
| 2 |
∴VE-CFD=
| 1 |
| 3 |
5
| ||
| 2 |
VC-EFD=VE-CFD∴h=
| 12 |
| 5 |
∴点C到平面DEF的距离为
| 12 |
| 5 |
点评:本题考查点到平面的距离的求法,等体积法的应用,考查平面垂直的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
相关题目
“0<x<2”是“x2-x<0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
利用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=4的值的时候需要做乘法和加法的次数分别为( )??
| A、6?6 | B、5?6 |
| C、5?5 | D、6?5 |
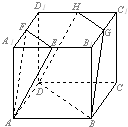 如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,
如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,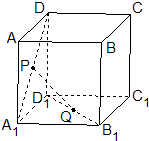 正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.
正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.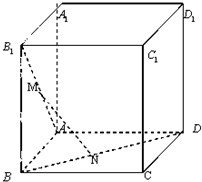 如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<
如图在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段AB1和BD上的点,且AM=BN=t(0<t<