题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,|φ|<π)的图象的一个最高点为(-
,2)与之相邻的与x轴的一个交点为(
,0).
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调减区间和函数图象的对称轴方程;
(3)用“五点法”作出函数y=f(x)在长度为一个周期区间上的图象.
| π |
| 12 |
| π |
| 6 |
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调减区间和函数图象的对称轴方程;
(3)用“五点法”作出函数y=f(x)在长度为一个周期区间上的图象.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象
专题:计算题,综合题,三角函数的图像与性质
分析:(1)依题意,知A=2,
=
,于是可求得ω=2;f(x)=2sin(2x+φ)过点(-
,2),|φ|<π,可求得φ,从而可得函数y=f(x)的解析式;
(2)利用正弦函数的单调性与对称性可求得函数y=f(x)的单调减区间和函数图象的对称轴方程;
(3)令2x+
取0,
,π,
,2π,得到对于的自变量x的值及函数值y的值,列表,描点、作图即可.
| T |
| 4 |
| π |
| 4 |
| π |
| 12 |
(2)利用正弦函数的单调性与对称性可求得函数y=f(x)的单调减区间和函数图象的对称轴方程;
(3)令2x+
| 2π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
解答:
(1)由题意,A=2,
=
-(-
)=
,
∴T=
=π,ω=2,
∴f(x)=2sin(2x+φ),将(-
,2)代入,得sin(-
+φ)=1,
∵|φ|<π,故φ=
,
∴函数y=f(x)的解析式为f(x)=2sin(2x+
).
(2)由
+2kπ≤2x+
≤
+2kπ(k∈Z),得-
+kπ≤x≤
+kπ(k∈Z),
∴函数的单调减区间是[-
+kπ,
+kπ](k∈Z);
由2x+
=
+kπ(k∈Z),得x=
-
(k∈Z),
∴函数图象的对称轴方程为x=
-
(k∈Z).
(3)①列表
②描点画图

| T |
| 4 |
| π |
| 6 |
| π |
| 12 |
| π |
| 4 |
∴T=
| 2π |
| ω |
∴f(x)=2sin(2x+φ),将(-
| π |
| 12 |
| π |
| 6 |
∵|φ|<π,故φ=
| 2π |
| 3 |
∴函数y=f(x)的解析式为f(x)=2sin(2x+
| 2π |
| 3 |
(2)由
| π |
| 2 |
| 2π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
∴函数的单调减区间是[-
| π |
| 12 |
| 5π |
| 12 |
由2x+
| 2π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
∴函数图象的对称轴方程为x=
| kπ |
| 2 |
| π |
| 12 |
(3)①列表
| x | -
|
-
|
|
|
| ||||||||||
2x+
|
0 |
|
π |
|
2π | ||||||||||
| y | 0 | 2 | -2 | 0 | 2 |

点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查五点法作函数y=Asin(ωx+φ)的图象,考查正弦函数的单调性与对称性的综合应用,属于难题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
如果两个球的体积之比为1:8,那么两个球的表面积之比为( )
| A、8:27 | B、1:2 |
| C、1:4 | D、1:8 |
设a=log54,b=(log53)2,c=log45,则a,b,c的大小关系为( )
| A、a<c<b |
| B、b<a<c |
| C、a<b<c |
| D、b<c<a |
利用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=4的值的时候需要做乘法和加法的次数分别为( )??
| A、6?6 | B、5?6 |
| C、5?5 | D、6?5 |
已知两数-2与-5,则这两数的等比中项是( )
A、
| ||
B、-
| ||
C、±
| ||
| D、不存在 |
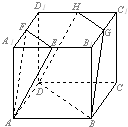 如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,
如图,E,F,G,H分别为正方体AC1的棱A1B1,A1D1,B1C1,D1C1的中点,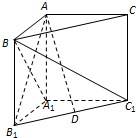 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.