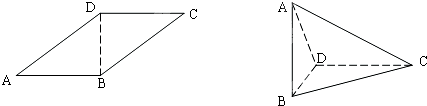题目内容
正方形ABCD中，M为AD中点，N为AB的中点，沿CM，CN分别将△CDM和△CBN折起，使CB与CD重合，设B点与D点重合于P点，DM的中点折起后变成PM的中点T，则异面直线CT和PN所成角的余弦值为 ．
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：取AN中点S，由已知得PN⊥PT，又PN⊥PC，从而PN⊥平面CMP．由此能求出异面直线CT和PN所成角的余弦值．
解答：
解：取AN中点S，
∵PN2+PT2=TS2+SM2=TN2，
∴PN⊥PT，
又PN⊥PC，
∴PN⊥平面CMP．
又CT?平面CMP，
∴PN⊥CT，
∴异面直线CT和PN所成角的余弦值为0．
故答案为：0．
解：取AN中点S，∵PN2+PT2=TS2+SM2=TN2，
∴PN⊥PT，
又PN⊥PC，
∴PN⊥平面CMP．
又CT?平面CMP，
∴PN⊥CT，
∴异面直线CT和PN所成角的余弦值为0．
故答案为：0．
点评：本题考查异面直线CT与PN所成角的余弦值的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
下列命题中，真命题为（ ）
| A、若x2=1，则x=1 | ||||
B、若
| ||||
C、若x=y，则
| ||||
| D、若x2＜y2，则x＜y |
已知函数f（x）=
x2+4lnx，若存在满足1≤x0≤3的实数x0，使得曲线f（x）在点（x0，f（x0））处的切线与直线x+my-10=0垂直，则实数m的取值范围是（ ）
| 1 |
| 2 |
| A、[5，+∞） | ||
| B、[4，5] | ||
C、[4，
| ||
| D、（-∞，4] |
如图，一个质点从原点出发，在与x轴、y轴平行的方向按（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→（2，1）→（2，2）→（1，2）…的规律向前移动，且每秒钟移动一个单位长度，那么到第2014秒时，这个质点所处位置的坐标是（ ）| A、（10，44） |
| B、（11，44） |
| C、（44，10） |
| D、（44，11） |