题目内容
已知函数f(x)=
x2+4lnx,若存在满足1≤x0≤3的实数x0,使得曲线f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
| 1 |
| 2 |
| A、[5,+∞) | ||
| B、[4,5] | ||
C、[4,
| ||
| D、(-∞,4] |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求出函数的导数,求出切线的斜率,再由两直线垂直斜率之积为-1,得到x0+
=m,再由基本不等式求出左边的最小值,代入端点1和3,比较得到最大值.
| 4 |
| x0 |
解答:
解:函数f(x)=
x2+4lnx的导数为f′(x)=x+
(x>0).
曲线f(x)在点(x0,f(x0))处的切线斜率为x0+
,
由于切线垂直于直线x+my-10=0,则有x0+
=m,
由于1≤x0≤3,则由x0+
≥2
=4,当且仅当x0=2∈[1,3],取得最小值4;
当x0=1时,取得最大值5.
故m的取值范围是[4,5].
故选:B.
| 1 |
| 2 |
| 4 |
| x |
曲线f(x)在点(x0,f(x0))处的切线斜率为x0+
| 4 |
| x0 |
由于切线垂直于直线x+my-10=0,则有x0+
| 4 |
| x0 |
由于1≤x0≤3,则由x0+
| 4 |
| x0 |
x0•
|
当x0=1时,取得最大值5.
故m的取值范围是[4,5].
故选:B.
点评:本题考查导数的几何意义:曲线在某点处的切线的斜率,考查两直线垂直的条件和基本不等式的运用,属于中档题.

练习册系列答案
相关题目
已知集合A={x|-1<x<3},B={x|log2x<2},则A∩B=( )
| A、(-1,3) |
| B、(0,4) |
| C、(0,3) |
| D、(-1,4) |
已知a=sin
,b=cos
,c=1,则a,b,c的大小顺序为( )
| 3 |
| 4 |
| 3 |
| 4 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、c<a<b |
函数f(x)=
+
,x∈(0,
]的最小值是( )
| sinx |
| 2 |
| 2 |
| sinx |
| π |
| 2 |
| A、2 | ||
| B、1 | ||
C、
| ||
| D、不存在 |
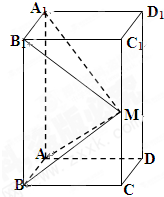 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点