题目内容
设函数f(x)=ax-a-x(a>0且a≠1).
(Ⅰ)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(Ⅱ)若f(1)=
,且g(x)=a2x+a-2x-2mf(x),且g(x)在[1,+∞)上的最小值为-2,求m的值.
(Ⅰ)若f(1)>0,试求不等式f(x2+2x)+f(x-4)>0的解集;
(Ⅱ)若f(1)=
| 3 |
| 2 |
考点:函数的最值及其几何意义,指、对数不等式的解法
专题:函数的性质及应用
分析:(1)先研究函数的单调性,结合指数函数的性质进行研究;
(2)先换元,将问题转化为二次函数的问题来求解.
(2)先换元,将问题转化为二次函数的问题来求解.
解答:
解:(I)∵f(1)>0,∴a-
>0,又a>0且a≠1,∴a>1,f(x)=ax-a-x
∴f(x)在R上为增函数,又f(-x)=a-x-ax=-f(x),故该函数为奇函数;
因此原不等式可化为:f(x2+2x)>f(4-x),结合单调性得
x2+2x>4-x,即x2+3x-4>0,
解得x>1或x<4,所以不等式解集为{x|x>1或x<4}.
(II)∵f(1)=
,∴a-
=
,即2a2-3a-2=0,解得a=2或a=-
(舍去)
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x为增函数∵x≥1,∴t≥f(1)=
,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
)
若m≥
,当t=m时,h(t)min=2-m2=-2,∴m=2
若m<
,当t=
时,h(t)min=
-3m=-2,解得m=
>
,舍去
综上可知m=2.
| 1 |
| a |
∴f(x)在R上为增函数,又f(-x)=a-x-ax=-f(x),故该函数为奇函数;
因此原不等式可化为:f(x2+2x)>f(4-x),结合单调性得
x2+2x>4-x,即x2+3x-4>0,
解得x>1或x<4,所以不等式解集为{x|x>1或x<4}.
(II)∵f(1)=
| 3 |
| 2 |
| 1 |
| a |
| 3 |
| 2 |
| 1 |
| 2 |
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x为增函数∵x≥1,∴t≥f(1)=
| 3 |
| 2 |
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
| 3 |
| 2 |
若m≥
| 3 |
| 2 |
若m<
| 3 |
| 2 |
| 3 |
| 2 |
| 17 |
| 4 |
| 25 |
| 12 |
| 3 |
| 2 |
综上可知m=2.
点评:利用函数的单调性解有些不等式往往能够将问题化繁为简,要注意和奇偶性相结合;涉及到指数式、对数式有关的稍稍复杂的不等式要注意能否采用换元法求解.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
给出下列定义:
①对于函数f(x),若存在x0∈R使f(x0)=x0成立,则称x0为函数f(x)的不动点;
②若函数的定义域区间与值域区间完全相同,则称该区间为函数的保值区间.
设函数f(x)=x2-2ax+a2+a(x∈R),则该函数有( )
①对于函数f(x),若存在x0∈R使f(x0)=x0成立,则称x0为函数f(x)的不动点;
②若函数的定义域区间与值域区间完全相同,则称该区间为函数的保值区间.
设函数f(x)=x2-2ax+a2+a(x∈R),则该函数有( )
| A、一个不动点和一个保值区间 |
| B、两个不动点和一个保值区间 |
| C、两个不动点和两个保值区间 |
| D、两个不动点和三个保值区间 |
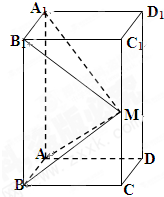 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点