题目内容
12.函数y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x-1.(1)求f(x)的函数解析式;
(2)写出函数f(x)的单调区间及最值;
(3)当关于x的方程f(x)=m有四个不同的解时,求m的取值范围.
分析 (1)当x<0时,-x>0,由已知中当x≥0时,f(x)=x2-2x-1,及函数f(x)是定义在R上的偶函数,可求出当x<0时函数的解析式,进而得到答案,
(2)由二次函数的图象画法可得到函数的草图;根据图象写出函数f(x)的单调区间及最值;
(3)由图象可得结论.
解答 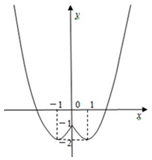 解:(1)当x<0时,-x>0,
解:(1)当x<0时,-x>0,
则当x≥0时,f(x)=x2-2x-1,
则f(-x)=(-x)2-2(-x)-1=x2+2x-1,
∵f(x)是偶函数,∴f(-x)=f(x)=x2+2x-1,
∴$f(x)=\left\{{\begin{array}{l}{{x^2}-2x-1,x≥0}\\{{x^2}+2x-1,x<0}\end{array}}\right.$;
(2)单调增区间为[-1,0]和(1,+∞),单调减区间为(-∞,-1]和[0,1];
当x=1或x=-1时,f(x)有最小值-2,无最大值;
(3)关于x的方程f(x)=m有四个不同的解,即有直线y=m与y=f(x)的图象有四个交点,由图象可知,m的取值范围是(-2,-1).
点评 本题考查的知识点是函数图象,函数的单调区间,函数的值域,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
2.如图是某多面体的三视图,网格纸上小正方形的边长为1,则该多面体的体积为( )
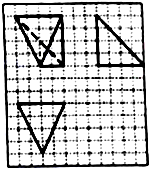

| A. | 32 | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{32}{3}$ |
3.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338石 | C. | 169石 | D. | 134石 |
7.函数y=sin2x图象上的某点P($\frac{π}{12}$,m)可以由函数y=cos(2x-$\frac{π}{4}$)上的某点Q向左平移n(n>0)个单位长度得到,则mn的最小值为( )
| A. | $\frac{5π}{24}$ | B. | $\frac{5π}{48}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{12}$ |
1.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{0}&{x=1}\\{|lg|x-1||}&{x≠1}\end{array}\right.$,则关于x的方程f2(x)+bf(x)+c=0有7个不同实数解的充要条件是( )
| A. | b<0且c>0 | B. | b>0且c<0 | C. | b<0且c=0 | D. | b>0且c=0 |
2.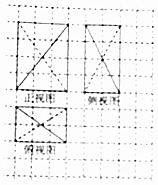 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )| A. | 24π | B. | 29π | C. | 48π | D. | 58π |
 如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.
如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.