设函数f(x)=$\left\{\begin{array}{l}{2^x}+1.x＞3\\{4^x}-4.x≤3\end{array}$.若f.且a≠2.则f(2a)=122．题目和参考答案——青夏教育精英家教网—

题目内容

17．设函数f（x）=$\left\{\begin{array}{l}{2^x}+1，x＞3\\{4^x}-4，x≤3\end{array}$，若f（a）=f（2），且a≠2，则f（2a）=122．

分析求出f（2）的值，根据函数的解析式求出a的值，求出2a，从而求出f（2a）的值即可．

解答解：f（2）=16-4=12，
故f（a）=12，
而a≠2，
故2^a+1=12，
解得：a=log₂11＞3，
故2a=log₂121＞3，
故f（2a）=f（log₂121）=${2}^{{log}_{2}121}$+1=121+1=122，
故答案为：122．

点评本题考查了函数求值问题，考查分段函数以及对数的运算，是一道基础题．

练习册系列答案

天天练习王口算题卡口算速算巧算系列答案

8．已知a＜0，函数$f（x）=acosx+\sqrt{1+sinx}+\sqrt{1-sinx}$，其中$x∈[{-\frac{π}{2}\;，\;\;\frac{π}{2}}]$．
（1）设$t=\sqrt{1+sinx}+\sqrt{1-sinx}$，求t的取值范围，并把f（x）表示为t的函数g（t）；
（2）求函数f（x）的最大值（可以用a表示）；
（3）设a=-1，若对区间$[{-\frac{π}{2}\;，\;\;\frac{π}{2}}]$内的任意x₁，x₂，若有|f（x₁）-f（x₂）|≤m，求实数m的取值范围．

5．准线方程为y=4的抛物线的标准方程是（　　）

12．函数y=f（x）是定义在R上的偶函数，当x≥0时，f（x）=x²-2x-1．
（1）求f（x）的函数解析式；
（2）写出函数f（x）的单调区间及最值；
（3）当关于x的方程f（x）=m有四个不同的解时，求m的取值范围．

2．过点P（1，-2）的直线l与圆C：（x-2）²+（y+3）²=9交于A，B两点，当∠ACB最小时，直线l的方程为（　　）

9．

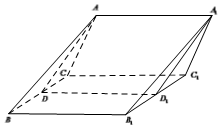如图三棱柱ABC-A₁B₁C₁，AB=BC=CA，D，D₁分别是BC，B₁C₁的中点，四边形ADD₁A₁是菱形，且平面ADD₁A₁⊥平面CBB₁C₁．
（Ⅰ）求证：四边形CBB₁C₁为矩形；
（Ⅱ）若$∠AD{D_1}=\frac{π}{3}$，且A-BB₁C₁C体积为$\sqrt{3}$，求三棱柱ABC-A₁B₁C₁的侧面积．

6．若复数z满足$\frac{\overline z}{1+i}=i$，其中i为虚数单位，则z=（　　）

7．

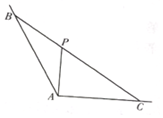如图，∠BAC=$\frac{2π}{3}$，P为∠BAC内部一点，过点P的直线与∠BAC的两边交于点B，C，且PA⊥AC，AP=$\sqrt{3}$．
（Ⅰ）若AB=3，求PC；
（Ⅱ）求$\frac{1}{PB}$$+\frac{1}{PC}$的取值范围．

试题分类