题目内容
2.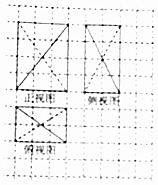 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )| A. | 24π | B. | 29π | C. | 48π | D. | 58π |
分析 根据几何体的三视图,得出该几何体是由长方体截割去4个等体积的三棱锥所得到的几何体,由此求出几何体的外接球的表面积.
解答 解:根据几何体的三视图,得:
该几何体是由长方体截割得到,如图中三棱锥A-BCD,
由三视图中的网络纸上小正方形边长为1,
得该长方体的长、宽、高分别为3、2、4,体对角线长为$\sqrt{9+4+16}$=$\sqrt{29}$
则几何体外接球的表面积为$4π•(\frac{\sqrt{29}}{2})^{2}$=29π.
故选:B.
点评 本题考查了利用空间几何体的三视图求几何体的外接球的表面积的应用问题,是基础题目.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
13.已知α是第二象限角,且3sinα+4cosα=0,则tan$\frac{α}{2}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
17.已知集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|y=lg(x-2x2)},则∁R(A∩B)=( )
| A. | [0,$\frac{1}{2}$) | B. | (-∞,0)∪[$\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | (-∞,0]∪[$\frac{1}{2}$,+∞) |
14.在($\sqrt{x}$-1)4•(x-1)2的展开式中,x项的系数为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
12.已知集合A={x|0<x≤3,x∈N},B={x|y=$\sqrt{{x}^{2}-1}$},则集合A∩B为( )
| A. | {1,2} | B. | {1,2,3} | C. | {0,1,2} | D. | {0,1,2,3} |
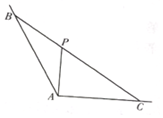 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.