题目内容
4.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于$\frac{\sqrt{6}}{4}$.分析 根据正三棱柱及线面角的定义知,取A1C1的中点D1,∠B1AD1是所求的角,再由已知求出正弦值.
解答 解:取A1C1的中点D1,连接B1D1,AD1,
在正三棱柱ABC-A1B1C1中,B1D1⊥面ACC1A1,
则∠B1AD1是AB1与侧面ACC1A1所成的角,
∵正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,
∴sin∠B1AD1=$\frac{{B}_{1}{D}_{1}}{A{B}_{1}}$=$\frac{\frac{\sqrt{3}}{2}AB}{\sqrt{2}AB}$=$\frac{\sqrt{6}}{4}$,
故答案为:$\frac{\sqrt{6}}{4}$.
点评 本题主要考查了线面角问题,求线面角关键由题意过线上一点作出面的垂线,再求线面角的正弦值,是中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.已知α是第二象限角,且3sinα+4cosα=0,则tan$\frac{α}{2}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
14.在($\sqrt{x}$-1)4•(x-1)2的展开式中,x项的系数为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |

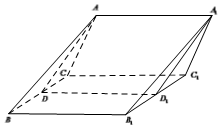 如图三棱柱ABC-A1B1C1,AB=BC=CA,D,D1分别是BC,B1C1的中点,四边形ADD1A1是菱形,且平面ADD1A1⊥平面CBB1C1.
如图三棱柱ABC-A1B1C1,AB=BC=CA,D,D1分别是BC,B1C1的中点,四边形ADD1A1是菱形,且平面ADD1A1⊥平面CBB1C1.