题目内容
7.函数y=sin2x图象上的某点P($\frac{π}{12}$,m)可以由函数y=cos(2x-$\frac{π}{4}$)上的某点Q向左平移n(n>0)个单位长度得到,则mn的最小值为( )| A. | $\frac{5π}{24}$ | B. | $\frac{5π}{48}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{12}$ |
分析 先求得m=sin(2•$\frac{π}{12}$)=$\frac{1}{2}$,故把函数y=sin2x图象上的点P($\frac{π}{12}$,$\frac{1}{2}$),向右平移n个单位,可得Q($\frac{π}{12}$+n,$\frac{1}{2}$),根据Q在函数y=cos(2x-$\frac{π}{4}$)的图象上,求得n的最小值值,可得mn的最小值.
解答 解:函数y=sin2x图象上的某点P($\frac{π}{12}$,m)可以由函数y=cos(2x-$\frac{π}{4}$)上的某点
Q向左平移n(n>0)个单位长度得到,∴m=sin(2•$\frac{π}{12}$)=$\frac{1}{2}$.
故把函数y=sin2x图象上的点P($\frac{π}{12}$,$\frac{1}{2}$),向右平移n个单位,可得Q($\frac{π}{12}$+n,$\frac{1}{2}$),
根据Q在函数y=cos(2x-$\frac{π}{4}$)的图象上,
∴m=cos[2($\frac{π}{12}$+n)-$\frac{π}{4}$]=cos(2n-$\frac{π}{12}$)=$\frac{1}{2}$,∴应有 2n-$\frac{π}{12}$=$\frac{π}{3}$,∴n=$\frac{5π}{24}$,
则mn的最小值为 $\frac{5π}{48}$,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
17.用与球心距离为1的平面去截球所得的截面面积为π,则球的表面积为( )
| A. | 2π | B. | 4π | C. | 8π | D. | $\frac{8}{3}π$ |
18.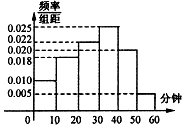 北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(1)根据已知条件完成如图列联表,并据此资料判断你是否有95%的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
 北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.| 非围棋迷 | 围棋迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(x2≥k0) | 0.05 | 0.010 |
| k0 | 3.74 | 6.63 |
2.已知函数f(x)=e2x-ax2+bx-1,其中a,b∈R,e为自然对数的底数,若f(1)=0,f′(x)是f(x)的导函数,函数f′(x)在区间(0,1)内有两个零点,则a的取值范围是( )
| A. | (e2-3,e2+1) | B. | (e2-3,+∞) | C. | (-∞,2e2+2) | D. | (2e2-6,2e2+2) |
17.已知集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|y=lg(x-2x2)},则∁R(A∩B)=( )
| A. | [0,$\frac{1}{2}$) | B. | (-∞,0)∪[$\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | (-∞,0]∪[$\frac{1}{2}$,+∞) |
