题目内容
若双曲线C:
-
=1(a>b>0)上的点P(
,y)到C的右焦点F2的距离小于它到C的左准线l的距离,则C的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3a |
| 2 |
A、(
| ||
B、(1,
| ||
| C、(2,+∞) | ||
| D、(1,2) |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的左右准线,判断P在右支上,运用双曲线的第二定义,得到|PF2|=ed=e(
-
),再由条件得到不等式,结合离心率公式,解不等式即可得到e的范围.
| 3a |
| 2 |
| a2 |
| c |
解答:
解:双曲线C:
-
=1的左、右准线方程为x=±
,
由于P的横坐标大于0,则P在右支上,
由双曲线的定义可得e=
(d为P到右准线的距离),
即有|PF2|=ed=e(
-
),
P到左准线的距离为
+
,
由条件得,e(
-
)<
+
,
由e=
,则有e(
-
)<
+
,
化简得,3e2-5e-2<0,
解得-
<e<2,
但e>1,则有1<e<2.
故选D.
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
由于P的横坐标大于0,则P在右支上,
由双曲线的定义可得e=
| |PF2| |
| d |
即有|PF2|=ed=e(
| 3a |
| 2 |
| a2 |
| c |
P到左准线的距离为
| 3a |
| 2 |
| a2 |
| c |
由条件得,e(
| 3a |
| 2 |
| a2 |
| c |
| 3a |
| 2 |
| a2 |
| c |
由e=
| c |
| a |
| 3 |
| 2 |
| 1 |
| e |
| 3 |
| 2 |
| 1 |
| e |
化简得,3e2-5e-2<0,
解得-
| 1 |
| 3 |
但e>1,则有1<e<2.
故选D.
点评:本题考查双曲线的定义、方程和性质,主要考查双曲线的离心率的求法,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
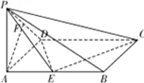 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,若二面角P-CD-A为60°,且AD=2,AB=4.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,若二面角P-CD-A为60°,且AD=2,AB=4.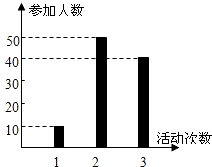 某校高一学生积极参加社会公益活动,成立了公益社,公益社共100人,据统计,他们在今年三月参加公益活动的次数统计如图所示,
某校高一学生积极参加社会公益活动,成立了公益社,公益社共100人,据统计,他们在今年三月参加公益活动的次数统计如图所示,