题目内容
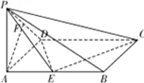 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,若二面角P-CD-A为60°,且AD=2,AB=4.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,若二面角P-CD-A为60°,且AD=2,AB=4.(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求直线PA与平面PED所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取PC中点M,连接FM,EM,根据线面平行的判定定理只需证明AF∥EM;
(Ⅱ)首先证明∠PDA就是二面角P-CD-A的平面角,在根据解三角形,求得PD=PE,取DE的中点G,连接AG,PG,得到∠PGA就是直线PA与平面PED所成角,再解三角形即可
(Ⅱ)首先证明∠PDA就是二面角P-CD-A的平面角,在根据解三角形,求得PD=PE,取DE的中点G,连接AG,PG,得到∠PGA就是直线PA与平面PED所成角,再解三角形即可
解答:
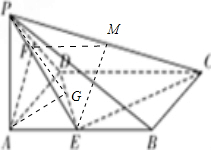 解:(Ⅰ)取PC中点M,连接FM,EM,
解:(Ⅰ)取PC中点M,连接FM,EM,
∵F、M分别为PD、PC的中点,∴FM∥DC,FM=
DC,
又E为AB的中点,∴AE∥DC,AE=DC,
∴AE∥FM,AE=
FM,∴四边形AFME为平行四边形,
∴AF∥ME,又AF?平面PEC,ME?平面PEC,
∴AF∥平面PEC.
(Ⅱ)∵PA⊥平面ABCD,PA?平面PAD
∴平面PAD⊥平面ABCD,
∵底面ABCD是矩形,
∴AB∥CD,CD⊥AD,AD⊥CD
∴CD⊥PD,
∴∠PDA就是二面角P-CD-A的平面角,
即∠PDA=60°,
∵AD=2,
∴PA=2
,PD=4,
又∵AE=
AB=2,
∴PE=
=4,
∴PD=PE,
取DE的中点G,连接AG,PG,
∴PG⊥DE,AG⊥DE,
∴∠PGA就是直线PA与平面PED所成角,
在Rt△ADE中,AG=
AD=
,
在Rt△PAG中,PG=
=
,
∴sin∠PGA=
=
=
 解:(Ⅰ)取PC中点M,连接FM,EM,
解:(Ⅰ)取PC中点M,连接FM,EM,∵F、M分别为PD、PC的中点,∴FM∥DC,FM=
| 1 |
| 2 |
又E为AB的中点,∴AE∥DC,AE=DC,
∴AE∥FM,AE=
| 1 |
| 2 |
∴AF∥ME,又AF?平面PEC,ME?平面PEC,
∴AF∥平面PEC.
(Ⅱ)∵PA⊥平面ABCD,PA?平面PAD
∴平面PAD⊥平面ABCD,
∵底面ABCD是矩形,
∴AB∥CD,CD⊥AD,AD⊥CD
∴CD⊥PD,
∴∠PDA就是二面角P-CD-A的平面角,
即∠PDA=60°,
∵AD=2,
∴PA=2
| 3 |
又∵AE=
| 1 |
| 2 |
∴PE=
| PA2+AE2 |
∴PD=PE,
取DE的中点G,连接AG,PG,
∴PG⊥DE,AG⊥DE,
∴∠PGA就是直线PA与平面PED所成角,
在Rt△ADE中,AG=
| ||
| 2 |
| 2 |
在Rt△PAG中,PG=
| PA2+AG2 |
| 14 |
∴sin∠PGA=
| PA |
| PG |
2
| ||
|
| ||
| 7 |
点评:本题考查线面平行、面面平行的判定及面面角,线面角的求解,考查学生的推理论证能力,解题关键是熟练掌握相关的定义、定理,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若双曲线C:
-
=1(a>b>0)上的点P(
,y)到C的右焦点F2的距离小于它到C的左准线l的距离,则C的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3a |
| 2 |
A、(
| ||
B、(1,
| ||
| C、(2,+∞) | ||
| D、(1,2) |

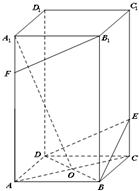 如图,在正四棱柱ABCD-A1B1C1D1中,点O是正方形ABCD对角线的交点,AA1=4,AB=2,点E,F分别在CC1和A1A上,且A1F=CE
如图,在正四棱柱ABCD-A1B1C1D1中,点O是正方形ABCD对角线的交点,AA1=4,AB=2,点E,F分别在CC1和A1A上,且A1F=CE