题目内容
曲线log2-|x|y=1与y=ax2（a＞0）无公共点，则a= ．
考点：函数的零点与方程根的关系
专题：数形结合,函数的性质及应用
分析：得出y=2-|x|，x∈（-2，2），x≠±1，画出图象，得出y=ax2（a＞0）过（1，1）（-1，1）点，即可求解a的值．
解答：
解：∵log2-|x|y=1，
∴y=2-|x|，x∈（-2，2），x≠±1，
∵与y=ax2（a＞0）无公共点，
∴y=ax2（a＞0）过（1，1）（-1，1）点，
∴1=a，
即a=1，
故答案为；1
∴y=2-|x|，x∈（-2，2），x≠±1，
∵与y=ax2（a＞0）无公共点，
∴y=ax2（a＞0）过（1，1）（-1，1）点，
∴1=a，
即a=1，
故答案为；1
点评：运用图象判断特殊点，代入即可，考查了函数交点，函数零点问题求解即可，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
已知全集U=R，A={x|y=
}，则∁UA=（ ）
| 1 | ||
|
| A、[1，+∞） |
| B、（-∞，1） |
| C、（1，+∞） |
| D、（-∞，1] |
若双曲线C：
-
=1（a＞b＞0）上的点P（
，y）到C的右焦点F2的距离小于它到C的左准线l的距离，则C的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3a |
| 2 |
A、（
| ||
B、（1，
| ||
| C、（2，+∞） | ||
| D、（1，2） |
已知R是实数集，集合P={x|x2+2012x-2013＞0}，Q={y|y=
}，则（∁RP）∩Q=（ ）
| -x2+2x+3 |
| A、（0，1] |
| B、[0，1] |
| C、（-1，1] |
| D、[-1，1] |
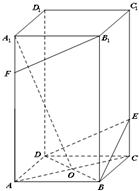如图，在正四棱柱ABCD-A1B1C1D1中，点O是正方形ABCD对角线的交点，AA1=4，AB=2，点E，F分别在CC1和A1A上，且A1F=CE