题目内容
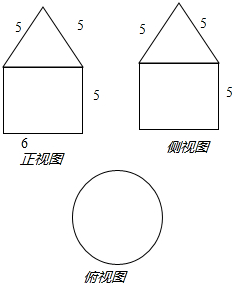 求几何体的体积.
求几何体的体积.考点:由三视图求面积、体积
专题:计算题
分析:由三视图得此几何体的几何特征:上圆锥、下圆柱,并求出圆柱、圆锥的底面半径和高,由体积公式计算出几何体的体积.
解答:
解:由三视图知几何体是一个简单组合体:上圆锥、下圆柱组成,
且圆柱的底面半径是3、高是5;
圆锥的底面半径是3、母线长是5,高h=
=4,
所以几何体的体积V=
×π×9×4+π×9×5=57π.
且圆柱的底面半径是3、高是5;
圆锥的底面半径是3、母线长是5,高h=
| 52-32 |
所以几何体的体积V=
| 1 |
| 3 |
点评:本题考查由三视图求体积,解题的关键是熟练掌握三视图的作图规则,由三视图还原出实物图的几何特征及测度.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
过边长为2的正方形中心作直线l将正方形分为两个部分,将其中的一个部分沿直线l翻折到另一个部分上.则两个部分图形中不重叠的面积的最大值为( )
| A、2 | ||
B、2(3-
| ||
C、4(2-
| ||
D、4(3-2
|
已知抛物线C:y2=4x的焦点为F,过点F的直线l交抛物线于M,N两点,且|MF|=2|NF|,则直线l的斜率为( )
A、±
| ||||
B、±2
| ||||
C、±
| ||||
D、±
|
在数列{an}中,an>0,a1=
,如果an+1是1与
的等比中项,那么a1+
+
+
+…+
的值是( )
| 1 |
| 2 |
| 2anan+1+1 |
| 4-an2 |
| a2 |
| 22 |
| a3 |
| 32 |
| a4 |
| 42 |
| a100 |
| 1002 |
A、
| ||
B、
| ||
C、
| ||
D、
|
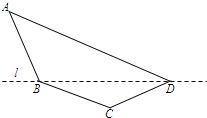 某单位设计一上展览沙盘,现谷在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
某单位设计一上展览沙盘,现谷在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.