题目内容
计算下列定积分:
(1)
4xdx
(2)
(x2-2x)dx
(3)
(
-1)dx;
(4)
(3x2-2x+1)dx;
(5)
(x-
)dx;
(6)
dx;
(7)
cosxdx;
(8)
sinxdx.
(1)
| ∫ | 5 0 |
(2)
| ∫ | 5 0 |
(3)
| ∫ | 2 1 |
| x |
(4)
| ∫ | 2 -1 |
(5)
| ∫ | 2 1 |
| 1 |
| x |
(6)
| ∫ | 2 1 |
| 1 |
| x2 |
(7)
| ∫ | π 0 |
(8)
| ∫ | 0 -π |
考点:定积分
专题:导数的综合应用
分析:直接根据定义计算即可.
解答:
解:(1)
4xdx=
d(2x2)=2(52-02)=50;
(2)
(x2-2x)dx=
d(
x3-x2)=(
×53-52)-(
×03-02)=
;
(3)
(
-1)dx=
d(
x
-x)=(
×2
-2)-(
×1
-1)=
(2
-1)-1=
;
(4)
(3x2-2x+1)dx=
d(x3-x2+x)=(23-22+2)-[(-1)3-(-1)2+(-1)]=9;
(5)
(x-
)dx=
d(
x2-lnx)=(
×22-ln2)-(
×12-ln1)=
-ln2;
(6)
dx=
d(-x-1)=-
+1=
;
(7)
cosxdx=
d(sinx)=sinπ-sin0=0;
(8)
sinxdx=
d(-cosx)=-cos0+cos(-π)=-2.
| ∫ | 5 0 |
| ∫ | 5 0 |
(2)
| ∫ | 5 0 |
| ∫ | 5 0 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 50 |
| 3 |
(3)
| ∫ | 2 1 |
| x |
| ∫ | 2 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
4
| ||
| 3 |
(4)
| ∫ | 2 -1 |
| ∫ | 2 -1 |
(5)
| ∫ | 2 1 |
| 1 |
| x |
| ∫ | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(6)
| ∫ | 2 1 |
| 1 |
| x2 |
| ∫ | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
(7)
| ∫ | π 0 |
| ∫ | π 0 |
(8)
| ∫ | 0 -π |
| ∫ | 0 -π |
点评:本题考查定积分的基本定义及运算,属基础题.

练习册系列答案
相关题目
在直角坐标系xOy中,设P是曲线C:xy=1(x>0)上任意一点,l是曲线C在点P处的切线,且l交坐标轴于A,B两点,则下列结论正确的是( )
| A、△OAB的面积为定值2 |
| B、△OAB的面积有最小值为3 |
| C、△OAB的面积有最大值为4 |
| D、△OAB的面积的取值范围是[3,4] |
用α表示一个平面,m表示一条直线,则α内一定有无数多条直线与m( )
| A、平行 | B、相交 | C、垂直 | D、异面 |
若执行如图所示的程序框图,则输出的结果s=( )


| A、8 | B、9 | C、10 | D、11 |
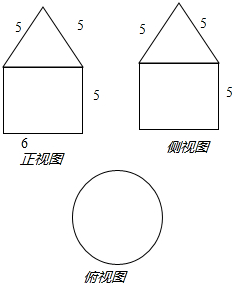 求几何体的体积.
求几何体的体积.