题目内容
已知f（x）=ax2+（a+1）x+（a-3），若它的图象过原点，则a= ．关于y轴对称，则a= ．
考点：二次函数的性质
专题：函数的性质及应用
分析：根据二次函数的性质分别求出满足条件的相对应的a的值即可．
解答：
解：①f（x）=ax2+（a+1）x+（a-3）的图象过原点，
把（0，0）代入得：a-3=0，从而a=3，
②若f（x）=ax2+（a+1）x+（a-3）的图象关于y轴对称，
则a+1=0，从而a=-1，
故答案为：3，-1．
把（0，0）代入得：a-3=0，从而a=3，
②若f（x）=ax2+（a+1）x+（a-3）的图象关于y轴对称，
则a+1=0，从而a=-1，
故答案为：3，-1．
点评：本题考查了二次函数的性质，牢记并理解其性质是解题的关键，是一道基础题．
练习册系列答案
相关题目
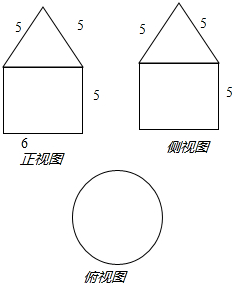求几何体的体积．