题目内容
已知抛物线C:y2=4x的焦点为F,过点F的直线l交抛物线于M,N两点,且|MF|=2|NF|,则直线l的斜率为( )
A、±
| ||||
B、±2
| ||||
C、±
| ||||
D、±
|
考点:直线与圆锥曲线的综合问题,抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:依题意F(1,0),设直线AB方程为x=my+1.将直线AB的方程与抛物线的方程联立,得y2-4my-4=0.由此能够求出直线AB的斜率.
解答:
解:依题意F(1,0),设直线AB方程为x=my+1.
将直线AB的方程与抛物线的方程联立,消去x得y2-4my-4=0.
设A(x1,y1),B(x2,y2),所以 y1+y2=4m,y1y2=-4.①
因为|MF|=2|NF|,
所以 y1=-2y2.②
联立①和②,消去y1,y2,得m=±
所以直线AB的斜率是±2
.
故选:B.
将直线AB的方程与抛物线的方程联立,消去x得y2-4my-4=0.
设A(x1,y1),B(x2,y2),所以 y1+y2=4m,y1y2=-4.①
因为|MF|=2|NF|,
所以 y1=-2y2.②
联立①和②,消去y1,y2,得m=±
| ||
| 4 |
所以直线AB的斜率是±2
| 2 |
故选:B.
点评:本题考查直线斜率的求法,抛物线的简单性质的应用,解题时要认真审题,仔细解答,注意挖掘题设中的条件,合理地进行等价转化.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
用α表示一个平面,m表示一条直线,则α内一定有无数多条直线与m( )
| A、平行 | B、相交 | C、垂直 | D、异面 |
已知实数a≥0,命题p,函数y=log2(x2+a)的定义域为R:命题q:x>0是x≥a+1成立的必要条件但不是充分条件,则( )
| A、p∧q为真命题 |
| B、(¬p)∧q为真命题 |
| C、p∨q为假命题 |
| D、p∨(¬q)为真命题 |
已知函数f(x)=2
sin(π-x)•cosx-1+2cos2x,其中x∈R,则下列结论中正确的是( )
| 3 |
A、f(x)的一条对称轴是x=
| ||||
B、f(x)在[-
| ||||
| C、f(x)是最小正周期为π的奇函数 | ||||
D、将函数y=2sin2x的图象左移
|
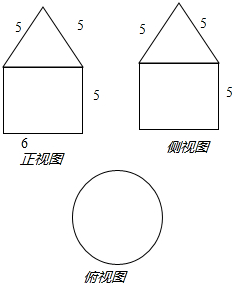 求几何体的体积.
求几何体的体积.