题目内容
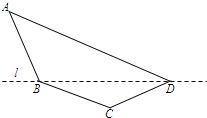 某单位设计一上展览沙盘,现谷在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
某单位设计一上展览沙盘,现谷在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.(1)设AB=x米,cosA=f(x),求f(x)的解析式,并指出x的取值范围;
(2)若四边形ABCD面积为6
| 3 |
考点:解三角形的实际应用,函数解析式的求解及常用方法
专题:综合题,导数的综合应用,解三角形
分析:(1)在△ABD与△CBD中,分别利用余弦定理,即可确定f(x)的解析式,及x的取值范围;
(2)四边形ABCD的面积S=
(AB•AD+CB•CD)sinA=
,构建函数g(x)=(x2-4)( x2-14x+49),x∈(2,5),求导函数,即可求得四边形ABCD面积的最大值,即可求x的值..
(2)四边形ABCD的面积S=
| 1 |
| 2 |
| (x2-4)(x2-14x+49) |
解答:
解:(1)设AB=x米,则BC=x米,CD=5-x米,AD=9-x米,
则有5-x>0,即x<5.
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC. …(3分)
因为∠A和∠C互补,所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA. …(5分)
即x2+(9-x)2-2 x(9-x)cosA=x2+(5-x)2+2 x(5-x)cosA.
解得cosA=
,即f(x)=
.
由余弦的定义,有
x<1,则x>2,
故x∈(2,5).…(8分)
(2)四边形ABCD的面积S=
(AB•AD+CB•CD)sinA=
[x(5-x)+x(9-x)]
=
.…(11分)
记g(x)=(x2-4)(x2-14x+49),x∈(2,5).
由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0,
∴x=4或x=7或x=-
.
∵x∈(2,5),∴x=4. …(14分)
所以函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.
所以S的最大值为6
.
属于四边形ABCD面积为6
时,x=4. …(16分)
则有5-x>0,即x<5.
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC. …(3分)
因为∠A和∠C互补,所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA. …(5分)
即x2+(9-x)2-2 x(9-x)cosA=x2+(5-x)2+2 x(5-x)cosA.
解得cosA=
| 2 |
| x |
| 2 |
| x |
由余弦的定义,有
| 2 |
故x∈(2,5).…(8分)
(2)四边形ABCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2A |
| (x2-4)(x2-14x+49) |
记g(x)=(x2-4)(x2-14x+49),x∈(2,5).
由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0,
∴x=4或x=7或x=-
| 1 |
| 2 |
∵x∈(2,5),∴x=4. …(14分)
所以函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.
所以S的最大值为6
| 3 |
属于四边形ABCD面积为6
| 3 |
点评:本题考查函数解析式,考查余弦定理的运用,考查四边形面积的计算,考查利用导数求函数的最值,正确表示四边形的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在2,0,1,5这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
用α表示一个平面,m表示一条直线,则α内一定有无数多条直线与m( )
| A、平行 | B、相交 | C、垂直 | D、异面 |
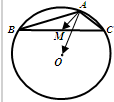 如图,O为△ABC的外心,AB=6,AC=4,∠BAC为钝角,M是边BC的中点,则
如图,O为△ABC的外心,AB=6,AC=4,∠BAC为钝角,M是边BC的中点,则| AM |
| AO |
| A、-10 | B、36 | C、16 | D、13 |
已知实数a≥0,命题p,函数y=log2(x2+a)的定义域为R:命题q:x>0是x≥a+1成立的必要条件但不是充分条件,则( )
| A、p∧q为真命题 |
| B、(¬p)∧q为真命题 |
| C、p∨q为假命题 |
| D、p∨(¬q)为真命题 |
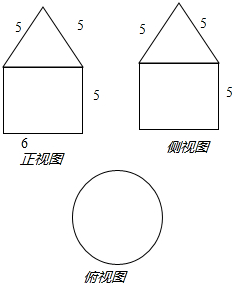 求几何体的体积.
求几何体的体积.