题目内容
求下列函数的单调区间:
(1)y=1+2sinx
(2)y=-3sinx.
(1)y=1+2sinx
(2)y=-3sinx.
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)直接写出正弦函数的单调期间得函数y=1+2sinx的单调期间;
(2)由函数y=-3sinx得单调性与y=sinx的单调性相反得答案.
(2)由函数y=-3sinx得单调性与y=sinx的单调性相反得答案.
解答:
解:(1)∵y=1+2sinx,
∴函数y=1+2sinx的单调性与函数y=sinx的单调性相同,
则函数增区间为[-
+2kπ,
+2kπ],k∈Z;减区间为[
+2kπ,
+2kπ],k∈Z.
(2)∵y=-3sinx,
∴函数y=-3sinx的单调性与y=sinx的单调性相反,
则函数的增区间为[
+2kπ,
+2kπ],k∈Z;减区间为[-
+2kπ,
+2kπ],k∈Z.
∴函数y=1+2sinx的单调性与函数y=sinx的单调性相同,
则函数增区间为[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
(2)∵y=-3sinx,
∴函数y=-3sinx的单调性与y=sinx的单调性相反,
则函数的增区间为[
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
点评:本题考查了与正弦函数有关的简单的复合三角函数的单调性,复合函数的单调性满足同增异减的原则,是基础题.

练习册系列答案
相关题目
在直角坐标系xOy中,设P是曲线C:xy=1(x>0)上任意一点,l是曲线C在点P处的切线,且l交坐标轴于A,B两点,则下列结论正确的是( )
| A、△OAB的面积为定值2 |
| B、△OAB的面积有最小值为3 |
| C、△OAB的面积有最大值为4 |
| D、△OAB的面积的取值范围是[3,4] |
若执行如图所示的程序框图,则输出的结果s=( )


| A、8 | B、9 | C、10 | D、11 |
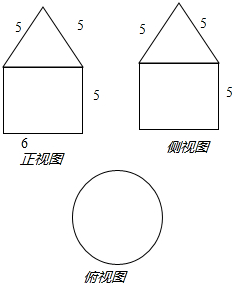 求几何体的体积.
求几何体的体积.