题目内容
已知tanβ=
,β∈(π,2π),求sinβ的值.
| 1 |
| 2 |
考点:同角三角函数间的基本关系
专题:三角函数的求值
分析:tanβ=
,β∈(π,2π),可得β∈(π,
).由
,解出即可.
| 1 |
| 2 |
| 3π |
| 2 |
|
解答:
解:∵tanβ=
,β∈(π,2π),
∴β∈(π,
).
∴
,解得
,
∴sinβ=-
.
| 1 |
| 2 |
∴β∈(π,
| 3π |
| 2 |
∴
|
|
∴sinβ=-
| ||
| 5 |
点评:本题考查了三角函数值所在象限的符号、同理三角函数基本关系式,考查了计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=2
sin(π-x)•cosx-1+2cos2x,其中x∈R,则下列结论中正确的是( )
| 3 |
A、f(x)的一条对称轴是x=
| ||||
B、f(x)在[-
| ||||
| C、f(x)是最小正周期为π的奇函数 | ||||
D、将函数y=2sin2x的图象左移
|
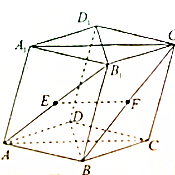 如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )
如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |
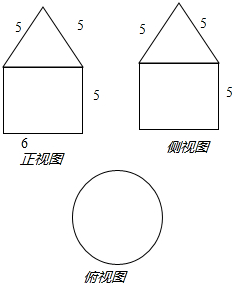 求几何体的体积.
求几何体的体积.