题目内容
对于平面α和两条不同的直线m，n，下列命题是真命题的是（ ）
| A、若m⊥α，n⊥α，则m∥n |
| B、若m∥α，n∥α则m∥n |
| C、若m⊥α，m⊥n则n∥α |
| D、若m，n与α所成的角相等，则m∥n |
考点：空间中直线与平面之间的位置关系
专题：操作型,空间位置关系与距离
分析：利用垂直于同一平面的两条直线平行，可知A正确；B，C列举所有情况即可判断；若m、n与 α所成的角相等，则m∥n，由线线平行的条件进行判断．
解答：
解：利用垂直于同一平面的两条直线平行，可知A正确；
若m∥α，n∥α则m∥n，m，n相交、异面都有可能，故B不正确；
若m⊥α，m⊥n则n与α平行，相交都有可能，故C不正确；
若m，n与α所成的角相等，则m∥n，此命题不正确，两异面的直线也可与同一平面成相等的线面角．
故选：A．
若m∥α，n∥α则m∥n，m，n相交、异面都有可能，故B不正确；
若m⊥α，m⊥n则n与α平行，相交都有可能，故C不正确；
若m，n与α所成的角相等，则m∥n，此命题不正确，两异面的直线也可与同一平面成相等的线面角．
故选：A．
点评：本题考查空间中直线与平面之间的位置关系，解答本题关键是熟练掌握线面间位置关系的判断条件以及较好的空间想像能力．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
已知函数f（x）=cos
，根据下列框图，输出S的值为（ ）
| πx |
| 3 |
| A、670 | ||
B、670
| ||
| C、671 | ||
| D、672 |
在△ABC中，角A，B，C的对边分别a，b，c，若a2+b2=
c2．则直线ax-by+c=0被圆x2+y2=9所截得的弦长为（ ）
| 1 |
| 2 |
A、2
| ||
B、3
| ||
C、2
| ||
D、3
|
定义在R上的偶函数f（x）满足f（x+1）f（x）=-2（f（x）≠0），且在区间（2013，2014）上单调递增，已知α，β是锐角三角形的两个内角，则f（sinα）、f（cosβ）的大小关系是（ ）
| A、f（sinα）＜f（cosβ） |
| B、f（sinα）＞f（cosβ） |
| C、f（sinα）=f（cosβ） |
| D、以上情况均有可能 |
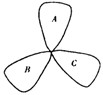荷花池中，有一只青蛙在成品字形的三片荷叶上跳来跳去（每次跳跃时，均从一叶跳到另一叶），而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图．假设现在青蛙在A叶上，则跳三次之后停在A叶上的概率是（ ）