题目内容
如图,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB、AD的夹角都是60°,N是CM的中点,设
=
,
=
,
=A
,试以
,
,
为基向量表示出向量
,并求BN的长.

| a |
| AB |
| b |
| AD |
| c |
| M |
| a |
| b |
| c |
| BN |

考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:由已知条件推导出
=
(
+
)=-
+
+
.由已知条件知|
|=|
|=2,|
|=3,
•
=0,
•
=
•
=3,由此利用
2=(-
+
+
)2能求出BN的长.
| BN |
| 1 |
| 2 |
| BC |
| BM |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| BN |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| c |
解答:
解:∵N是CM的中点,设
=
,
=
,
=A
,
底面ABCD是边长为2的正方形,
∴
=
(
+
)
=
(
+
+
)
=-
+
+
.
∵在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,
侧棱AM的长为3,且AM和AB、AD的夹角都是60°,
∴|
|=|
|=2,|
|=3,
•
=0,
•
=2×3×cos60°=3,
•
=2×3×cos60°=3,
∴
2=(-
+
+
)2
=1+1+
-
×3+
×3=
,
∴|
|=
,即BN的长为
.
| a |
| AB |
| b |
| AD |
| c |
| M |
底面ABCD是边长为2的正方形,
∴
| BN |
| 1 |
| 2 |
| BC |
| BM |
=
| 1 |
| 2 |
| AD |
| BA |
| AM |
=-
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| c |
∵在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,
侧棱AM的长为3,且AM和AB、AD的夹角都是60°,
∴|
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
∴
| BN |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| c |
=1+1+
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 4 |
∴|
| BN |
| ||
| 2 |
| ||
| 2 |
点评:本题考查向量的表示和线段长的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
对于平面α和两条不同的直线m,n,下列命题是真命题的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m∥α,n∥α则m∥n |
| C、若m⊥α,m⊥n则n∥α |
| D、若m,n与α所成的角相等,则m∥n |
已知集合U=R,集合A={x|-l≤x≤3},集合B=|x|log2x<2},则A∩B=( )
| A、{x|1≤x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|0<x≤3} |
| D、{x|-1≤x<0} |
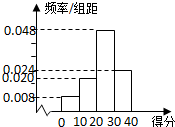 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下: