Question

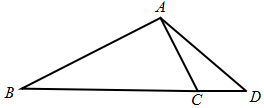
8．△ABC的内角A，B，C的对边分别为a，b，c，其中b≠c，
且bcosB=ccosC，延长线段BC到点D，使得BC=4CD=4，∠CAD=30°，
（Ⅰ）求证：∠BAC是直角；
（Ⅱ）求tan∠D的值．

Answer 1

分析 （Ⅰ）根据正弦定理以及二倍角公式即可证明，
（Ⅱ）如图所示：过点C做CE⊥AC，根据平行线分线段成比例定理，设CE=x，则AB=5x，AD=$\frac{5}{2}$x，再根据勾股定理可得x的值，再由正弦定理，sinD=$\frac{\sqrt{21}}{7}$，再根据同角的三角函数的关系即可求出答案．

解答 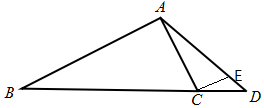解：（Ⅰ）证明：由正弦定理可得sinBcosB=sinCcosC，
即sin2B=sin2C，
∵b≠c，
∴2B+2C=180°，
∴B+C=90°，
∴∠BAC=180°-90°=90°，
（Ⅱ）：如图所示：过点C做CE⊥AC，
∵BC=4，BC=4CD，
∴CD=1，BD=5，
∵∠BAC=90°，
∴CE∥AB，
∴$\frac{CE}{AB}$=$\frac{DE}{AD}$=$\frac{CD}{BD}$=$\frac{1}{5}$，
设CE=x，则AB=5x，
∵∠CAD=30°，
∴AE=2x，AC=$\sqrt{3}$x，
∴$\frac{DE}{DE+2x}$=$\frac{1}{5}$，
∴DE=$\frac{1}{2}$x，
∵AB²+AC²=BC²，
∴25x²+3x²=16，
解得x=$\frac{2\sqrt{7}}{7}$，
在△CED中，∠CED=120°，CE=$\frac{2\sqrt{7}}{7}$，CD=1，
由正弦定理可得$\frac{CE}{sinD}$=$\frac{CD}{sin∠CED}$，
即sinD=$\frac{\frac{2\sqrt{7}}{7}×\frac{\sqrt{3}}{2}}{1}$=$\frac{\sqrt{21}}{7}$，
cosD=$\sqrt{1-si{n}^{2}D}$=$\frac{2\sqrt{7}}{7}$，
∴tanD=$\frac{sinD}{cosD}$=$\frac{\sqrt{3}}{2}$．

点评 本题考查了解三角形的有关知识以及平行线分线段成比例定理和正弦定理和同角的三角函数的关系，考查了学生的运算能力和转化能力，属于中档题．