题目内容
16.在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
(Ⅱ)若D,E在线段BC上,且BD=DE=EC,$AE=2\sqrt{3}BD$,求AD的长.
分析 (Ⅰ)根据正弦定理和两角和的正弦公式和三角形的面积公式即可求出,
(Ⅱ)设BD=x,由余弦定理求出x的值,再根据勾股定理即可求出.
解答  解:(Ⅰ)B=60°,c=4,b=6,
解:(Ⅰ)B=60°,c=4,b=6,
在△ABC中,由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$,
得$sinC=\frac{csinB}{b}=\frac{{4•\frac{{\sqrt{3}}}{2}}}{6}=\frac{{\sqrt{3}}}{3}$,
又b>c,所以B>C,则C为锐角,所以$cosC=\frac{{\sqrt{6}}}{3}$,
则sinA=sin(B+C)=sinBcosC+cosBsinC=$\frac{{\sqrt{3}}}{2}•\frac{{\sqrt{6}}}{3}+\frac{1}{2}•\frac{{\sqrt{3}}}{3}=\frac{{3\sqrt{2}+\sqrt{3}}}{6}$,
所以△ABC的面积$S=\frac{1}{2}bcsinA=12•\frac{{3\sqrt{2}+\sqrt{3}}}{6}=6\sqrt{2}+2\sqrt{3}$.
(Ⅱ)设BD=x,则BE=2x,$AE=2\sqrt{3}x$,又B=60°,c=4,
在△ABE中,由余弦定理得12x2=16+4x2-2•4•2x•cos60°,
即8x2=16-8x,解得x=1,
则BE=2,所以∠AEB=90°,
在直角△ADE中,$AD=\sqrt{A{E^2}+D{E^2}}=\sqrt{12+1}=\sqrt{13}$.
点评 本题考查了正弦定理和余弦定理和三角形的面积公式和两角和的正弦公式,考查了学生的运算能力和分析解决问题的能力,属于中档题

练习册系列答案
相关题目
6.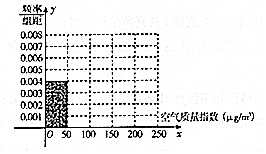 全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图求该组数据的平均数与中位数;
(3)在空气质量指数分别属于[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件A”两天空气都为良“发生的概率.
 全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3)区间 | [0,50) | [50,100) | [100,150) | [150,200) | [200,250) |
| 空间质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
(2)由频率分布直方图求该组数据的平均数与中位数;
(3)在空气质量指数分别属于[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件A”两天空气都为良“发生的概率.
7.已知等比数列{an}中,a3a9=2a52,且a3=2,则a5=( )
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
5.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与抛物线C2:y2=2px(p>0)的准线围成一个等边三角形,则双曲线C1的离心率是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
 △ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,
△ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,