Question

13．设D为△ABC的所在平面内一点，$\overrightarrow{BC}=-4\overrightarrow{CD}$，则$\overrightarrow{AD}$=（　　）

• A． $\frac{1}{4}\overrightarrow{AB}-\frac{3}{4}\overrightarrow{AC}$
• B． $\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$
• C． $\frac{3}{4}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$
• D． $\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$

Answer 1

分析 取BC的中点E，则D为CE的中点，用$\overrightarrow{AB}，\overrightarrow{AC}$表示出$\overrightarrow{AE}$即可得出$\overrightarrow{AD}$关于$\overrightarrow{AB}，\overrightarrow{AC}$的不等式．

解答 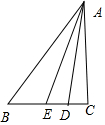解：∵$\overrightarrow{BC}=-4\overrightarrow{CD}$，∴D是BC的靠近C点的四等分点，
取BC的中点E，则D为CE的中点，
∴$\overrightarrow{AE}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$，$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AE}+\frac{1}{2}\overrightarrow{AC}$，
∴$\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$．
故选B．

点评 本题考查了平面向量的几何运算，属于中档题．