题目内容

19．若复数z=$\frac{3-i}{i}$的共轭复数为$\overline{z}$，则$\overline{z}$在复平面内的对应点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数的运算法则、共轭复数的定义、几何意义即可得出．

解答 解：复数z=$\frac{3-i}{i}$=$\frac{-i（3-i）}{-i•i}$=-3i-1的共轭复数为$\overline{z}$=-1+3i，则$\overline{z}$在复平面内的对应点（-1，3）位于第二象限．
故选：B．

点评 本题考查了复数的运算法则、共轭复数的定义、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
9．已知函数f（x）=sin2xcos$\frac{π}{5}-cos2xsin\frac{π}{5}$．
（Ⅰ）求函数f（x）的最小正周期和对称轴的方程；
（Ⅱ）求函数f（x）在区间$[0，\frac{π}{2}]$上的最大值．
10．由于渤海海域水污染严重，为了获得第一手的水文资料，潜水员需要潜入水深为60米的水底进行作业，根据经验，潜水员下潜的平均速度为v（米/单位时间），每单位时间消耗氧气${（\frac{v}{10}）^3}+1$（升），在水底作业10个单位时间，每单位时间消耗氧气0.9（升），返回水面的平均速度为$\frac{v}{2}$（米/单位时间），每单位时间消耗氧气1.5（升），记该潜水员完成此次任务的消耗氧气总量为y（升）．
（1）求y关于v的函数关系式；
（2）若c≤v≤15（c＞0），求当下潜速度v取什么值时，消耗氧气的总量最少．
7．已知等比数列{an}中，a3a9=2a52，且a3=2，则a5=（　　）
A．-4B．4C．-2D．2
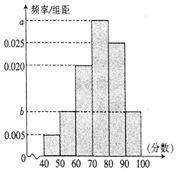14．某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图，其中前三段的频率成等比数列．
（1）求图中实数a的值；
（2）若该校高一年级共有学生640人，试估计该校高一年级期中考试数学成绩不低于80分的人数；
（3）若从样本中数学成绩在[40，50）与[90，100]两个分数段内的学生中随机选取两名学生，记这两名学生成绩在[90，100]内的人数为X，求随机变量X的分布列和期望值．
4．已知等差数列{an}中，a2=2，a12=-2，则{an}的前10项和为6．
11．若复数z满足z•（1+i）2=|1+i|2，则z=-i．
8．△ABC的内角A，B，C的对边分别为a，b，c，其中b≠c，
且bcosB=ccosC，延长线段BC到点D，使得BC=4CD=4，∠CAD=30°，
（Ⅰ）求证：∠BAC是直角；
（Ⅱ）求tan∠D的值．
8．已知函数f（x）=2cos22x-2，给出下列命题：
①?β∈R，f（x+β）为奇函数；
②?α∈（0，$\frac{3π}{4}$），f（x）=f（x+2α）对x∈R恒成立；
③?x1，x2∈R，若|f（x1）-f（x2）|=2，则|x1-x2|的最小值为$\frac{π}{4}$；
④?x1，x2∈R，若f（x1）=f（x2）=0，则x1-x2=kπ（k∈Z）．其中的真命题有（　　）
A．①②B．③④C．②③D．①④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网