题目内容
已知f(x)=ex(其中e为自然对数的底数),g(x)=
x+m(m,n∈R)且7<e2<
(1)若T(x)=f(x)g(x),m=1-
,求T(x)在[0,1]上最大值;
(2)若n=4时,方程f(x)=g(x)在[0,2]上恰有两个相等实根,求m的范围;
(3)若m=-
,n∈N*,求使f(x)图象恒在g(x)图象上方的最大正整数n.
| n |
| 2 |
| 15 |
| 2 |
(1)若T(x)=f(x)g(x),m=1-
| n |
| 2 |
(2)若n=4时,方程f(x)=g(x)在[0,2]上恰有两个相等实根,求m的范围;
(3)若m=-
| 15 |
| 2 |
考点:利用导数求闭区间上函数的最值,函数的零点
专题:综合题,导数的综合应用
分析:(1)m=1-
时,求得导数T'(x),分n≥0,n<-2,-2≤n<0三种情况进行讨论,可求得函数最大值;
(2)n=4时,方程f(x)=g(x)即为ex=2x+m,构造函数h(x)=ex-2x,x∈[0,2],则问题转化为h(x)与y=m图象的交点问题,借助导数可求函数最值、单调性,借助图象可得m范围;
(3)问题即为f(x)>g(x)恒成立,构造函数h(x)=ex-
x+
,由导数可求得h(x)的最小值h(x)min=h(ln
)=
-
ln
+
,则
-
ln
+
>0,令t(x)=x-xlnx+
(x>0),用导数可研究t(x)的单调性,根据单调性及e2范围可求得n的最大值;
| n |
| 2 |
(2)n=4时,方程f(x)=g(x)即为ex=2x+m,构造函数h(x)=ex-2x,x∈[0,2],则问题转化为h(x)与y=m图象的交点问题,借助导数可求函数最值、单调性,借助图象可得m范围;
(3)问题即为f(x)>g(x)恒成立,构造函数h(x)=ex-
| n |
| 2 |
| 15 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
解答:
解:(1)当m=1-
时,T(x)=f(x)g(x)=ex(
x+m)=ex(
x+1-
),
T'(x)=ex(
x+1-
)+
•ex=(
x+1)•ex,
①当n≥0时,x∈[0,1]时,T'(x)>0,T(x)在[0,1]上单调递增,T(x)max=T(1)=e;
②当0<-
<1,即n<-2时,x∈[0,-
)时,T'(x)>0,T(x)递增;x∈(-
,1]时,T'(x)<0,T(x)递减;
∴x=-
时T(x)取得极大值,也为最大值,T(x)max=T(-
)=-
•e-
;
③当-
≥1,即-2≤n<0时,x∈[0,1]时,T'(x)≥0,T(x)递增,
∴T(x)max=T(1)=e;
综上,当n≥-2时,T(x)max=e;当n<-2时,T(x)max=-
•e-
;
(2)n=4时,方程f(x)=g(x)即为ex=2x+m,
令h(x)=ex-2x,x∈[0,2],则h'(x)=ex-2,
当x∈[0,ln2)时,h'(x)<0,h(x)递减;当x∈(ln2,2]时,h'(x)>0,h(x)递增;
∴x=ln2时,h(x)取得极小值,也为最小值,h(x)min=h(ln2)=2-2ln2;
又h(0)=1,h(2)=e2-4>1,∴h(x)max=e2-4;
∵f(x)=g(x)在[0,2]上恰有两个相等实根,
∴m=2-2ln2或1<m≤e2-4.
(3)m=-
时,f(x)的图象恒在g(x)图象上方,即f(x)>g(x)恒成立,即ex>
x-
恒成立,
令h(x)=ex-
x+
,则h'(x)=ex-
,令h'(x)=0,得x=ln
,
当x<ln
时,h'(x)<0,h(x)递减,当x>ln
时,h'(x)>0,h(x)递增,
∴x=ln
时,h(x)取得极小值,也为最小值,h(x)min=h(ln
)=
-
ln
+
,
∵f(x)>g(x)恒成立,∴
-
ln
+
>0,
令t(x)=x-xlnx+
(x>0),则t'(x)=-lnx,
当0<x<1时,t'(x)>0,t(x)递增;当x>1时,t'(x)<0,t(x)递减;
当n=2e2时,t(e2)=e2-e2lne2+
=-e2+
,
又7<e2<
,∴t(e2)>0,由x>1时t(x)递减知t(14)>0,即n=14时,
-
ln
+
>0;
而
-
ln
+
=
-
ln
<
-
lne2=0,即n=15时,
-
ln
+
<0,
∴满足条件的最大正整数n=14.
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
T'(x)=ex(
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
①当n≥0时,x∈[0,1]时,T'(x)>0,T(x)在[0,1]上单调递增,T(x)max=T(1)=e;
②当0<-
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
∴x=-
| 2 |
| n |
| 2 |
| n |
| n |
| 2 |
| 2 |
| n |
③当-
| 2 |
| n |
∴T(x)max=T(1)=e;
综上,当n≥-2时,T(x)max=e;当n<-2时,T(x)max=-
| n |
| 2 |
| 2 |
| n |
(2)n=4时,方程f(x)=g(x)即为ex=2x+m,
令h(x)=ex-2x,x∈[0,2],则h'(x)=ex-2,
当x∈[0,ln2)时,h'(x)<0,h(x)递减;当x∈(ln2,2]时,h'(x)>0,h(x)递增;
∴x=ln2时,h(x)取得极小值,也为最小值,h(x)min=h(ln2)=2-2ln2;
又h(0)=1,h(2)=e2-4>1,∴h(x)max=e2-4;
∵f(x)=g(x)在[0,2]上恰有两个相等实根,
∴m=2-2ln2或1<m≤e2-4.
(3)m=-
| 15 |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
令h(x)=ex-
| n |
| 2 |
| 15 |
| 2 |
| n |
| 2 |
| n |
| 2 |
当x<ln
| n |
| 2 |
| n |
| 2 |
∴x=ln
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
∵f(x)>g(x)恒成立,∴
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
令t(x)=x-xlnx+
| 15 |
| 2 |
当0<x<1时,t'(x)>0,t(x)递增;当x>1时,t'(x)<0,t(x)递减;
当n=2e2时,t(e2)=e2-e2lne2+
| 15 |
| 2 |
| 15 |
| 2 |
又7<e2<
| 15 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
而
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 30 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 30 |
| 2 |
| 15 |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| 15 |
| 2 |
∴满足条件的最大正整数n=14.
点评:本题考查利用导数研究函数的最值、单调性及恒成立问题,考查分类讨论思想,考查学生综合运用知识分析问题解决问题的能力,综合性强,难度大,能力要求高.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
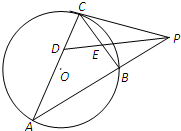 如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则
 若中心在原点的椭圆C1:
若中心在原点的椭圆C1: