Question

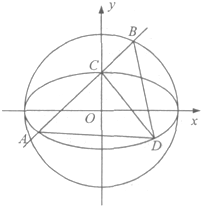若中心在原点的椭圆C₁：

x2

a2

+

y2

b2

=1（a＞b＞0）与双曲线x²-y²=2有共同的焦点，且它们的离心率互为倒数，圆C₂的直径是椭圆C₁的长轴，C是椭圆的上顶点，动直线AB过点C且与圆C₂交于A、B两点，CD垂直于AB交椭圆于点D．
（1）求椭圆C₁的方程；
（2）求△ABD面积的最大值，并求此时直线AB的方程．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（1）求出双曲线的截距，利用椭圆与双曲线的离心率关系求出椭圆的离心率，然后求出椭圆的长半轴，短半轴，即可求椭圆C₁的方程；
（2）设出直线方程，利用点到直线的距离，求出弦长，联立直线AB的方程与椭圆方程，求出三角形的面积，然后求解△ABD面积的最大值，即可求解此时直线AB的方程．

解答： （1）解：双曲线x²-y²=2的焦点为（±2，0），离心率为

2

，（2分），
椭圆的离心率为：

2

2

由题意，c=2，解得：a=2

2

．
∴b²=a²-c²=45
∴椭圆方程为

x2

8

+

y2

4

=1（4分）
（2）解：当直线AB斜率不存在时，不符合题意．
当AB斜率存在且不为0时，设直线AB的方程为y=kx+2，直线CD的方程为y=-

1

k

x+2
圆心（0，0）到直线AB的距离为d=

2

k2+1

（5分）
∴直线AB被圆C₂所截得的弦长|AB|=2

8-d2

=

4 2k2+1

k2+1

（6分）
由

x2 8 + y2 4 =1 y=- 1 k x+2

得：（k²+2）x²-8kx=0
∴xD=

8k

k2+2

，yD=-

1

k

×

8k

k2+2

+2=

2k2-4

k2+2

（7分）
故|CD|=

( 8k k2+2 )2+( 2k2-4 k2+2 -2)2

=

8 k2+1

k2+2

（8分）
∴S△ABD=

1

2

×

4 2k2+1

k2+1

×

8 k2+1

k2+2

=

16 2k2+1

k2+2

（9分）
令t=

2k2+1

，则k2=

t2-1

2

(t2＞1)
故S△ABD=

16t

t2-1 2 +2

=

32t

t2+3

=

32

t+ 3 t

≤

32

2 3

=

16 3

3

（11分）
当且仅当t=

3

t

，即t=

3

时，等号成立
此时

2k2+1

=

3

⇒k=±1（12分）
当直线AB斜率为0，即AB∥x轴时，S△ABD=8＜

16 3

3

∴△ABD面积的最大值为

16 3

3

，这时直线AB的方程为y=±x+1．（14分）

点评：本题考查椭圆的定义及其性质，双曲线的性质，求解椭圆的方程，直线与椭圆的位置关系，三角形面积的求法，考查分析问题解决问题的能力．