题目内容
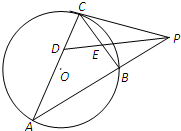如图，PC是圆O的切线，切点为C，直线PA与圆O交于A、B两点，∠APC的平分线分别交弦CA，CB于D，E两点，已知PC=3，PB=2，则| PE |
| PD |
考点：与圆有关的比例线段
专题：直线与圆
分析：由已知条件推导出△PCB∽△PAC，△PCE∽△PAD，由此能求出
=
=
．
| PE |
| PD |
| PC |
| PA |
| 2 |
| 3 |
解答：
解：作直线CF，连结BF，∴CF⊥PC，
∴∠PCB+∠BCF=90°，
∵CF是直径，∴∠BCF+∠F=90°，
∴∠PCB=∠F，∵∠F=∠A，∴∠PCB=∠A，
∴△PCB∽△PAC，
∴
=
=
，
∵∠PCE=∠PCB=∠A，∠CPE=∠APD，
∴△PCE∽△PAD，
∴
=
=
．
故答案为：
．
∴∠PCB+∠BCF=90°，
∵CF是直径，∴∠BCF+∠F=90°，
∴∠PCB=∠F，∵∠F=∠A，∴∠PCB=∠A，
∴△PCB∽△PAC，
∴
| PC |
| PA |
| PB |
| PC |
| 2 |
| 3 |
∵∠PCE=∠PCB=∠A，∠CPE=∠APD，
∴△PCE∽△PAD，
∴
| PE |
| PD |
| PC |
| PA |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查与圆有关的线段比值的求法，是中档题，解题时要认真审题，注意圆的性质的灵活运用．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
对于函数f(x)=cos2(x-
)+sin2(x+
)-1，下列选项中正确的是（ ）
| π |
| 12 |
| π |
| 12 |
A、f(x)在(
| ||||
| B、f（x）的图象关于原点对称 | ||||
| C、f（x）的最小正周期为2π | ||||
| D、f（x）的最大值为1 |
对于空间的两条直线m、n和一个平面α，下列命题中的真命题是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若m∥α，n?α，则m∥n |
| C、若m∥α，n⊥α，则m∥n |
| D、若m⊥α，n⊥α，则m∥n |