题目内容
已知函数f（x）=-2x2+|x|+1，若f（log2m）＞f（3），则实数m的取值范围是 ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：先判断函数f（x）的奇偶性和单调性，然后解不等式即可得到结论．
解答：
解：∵f（x）=-2x2+|x|+1，
∴f（-x）=-2x2+|x|+1=f（x），
即f（x）是偶函数，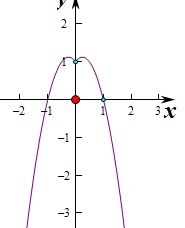
当x≥0时f（x）=-2x2+|x|+1=-2x2+x+1，对称轴为x=
，
此时函数在[3，+∞）上单调递减，
∴不等式f（log2m）＞f（3）等价为f（|log2m|）＞f（3），
即|log2m|＜3，
∴-3＜log2m＜3，
解得
＜m＜8，
故答案为：（
，8）
∴f（-x）=-2x2+|x|+1=f（x），
即f（x）是偶函数，
当x≥0时f（x）=-2x2+|x|+1=-2x2+x+1，对称轴为x=
| 1 |
| 4 |
此时函数在[3，+∞）上单调递减，
∴不等式f（log2m）＞f（3）等价为f（|log2m|）＞f（3），
即|log2m|＜3，
∴-3＜log2m＜3，
解得
| 1 |
| 8 |
故答案为：（
| 1 |
| 8 |
点评：本题主要考查不等式的解法，利用函数的奇偶性和单调性的性质，将不等式进行转化是解决本题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
已知△ABC的重心为G，内角A，B，C的对边分别为a，b，c，若a
+b
+
c
=
，则角A为（ ）
| GA |
| GB |
| ||
| 3 |
| GC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|