题目内容
有3个男生和3个女生参加某公司招聘,按随机顺序逐个进行面试,那么任何时候等待面试的女生人数都不少于男生人数的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:随机逐个面试共有6!种可能的顺序,而任何时候等待面试的女生人数都不少于男生人数的顺序可以分为5类,求出相应的顺序,即可求得概率.
解答:
解:随机逐个面试共有6!种可能的顺序,而任何时候等待面试的女生人数都不少于男生人数的顺序可以分为5类:
①男男男女女女,此时有
=36种;②男男女男女女,此时有
=36种;
③男男女女男女,此时有
=36种;④男女男男女女,此时有
=36种;
⑤男女男女男女,此时有
=36种;
故共有36×5=180种
故任何时候等待面试的女生人数都不少于男生人数的概率是
=
;
故答案为:
①男男男女女女,此时有
| A | 3 3 |
| A | 3 3 |
| A | 2 3 |
| A | 1 3 |
| A | 2 2 |
③男男女女男女,此时有
| A | 2 3 |
| A | 2 3 |
| A | 1 3 |
| A | 1 3 |
| 2 2 |
⑤男女男女男女,此时有
| A | 3 3 |
| A | 3 3 |
故共有36×5=180种
故任何时候等待面试的女生人数都不少于男生人数的概率是
| 180 |
| 6! |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查概率的计算,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合m={x∈Z|-x2+6x>0},N={x|x2-5<0},则M∩N等于( )
| A、{1,2,3} |
| B、{1,2} |
| C、{2,3} |
| D、{3,4} |
已知长方体的对角线长为4,过同一顶点的两条棱与此对角线成角均为60°,则长方体的体积是( )
A、16
| ||
B、8
| ||
C、8
| ||
D、4
|
有5条线段长度分别为1,3,5,7,9,从中任意取出3条,则所取3条线段可构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
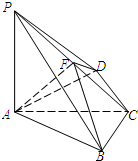 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.