题目内容
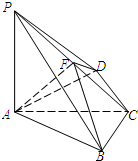 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.(1)求证:PB⊥BC;
(2)求点D到平面PCB的距离.
考点:直线与平面垂直的判定,直线与平面垂直的性质,点、线、面间的距离计算
专题:计算题,证明题,空间位置关系与距离
分析:(1)由余弦定理求得AB=2
,由AB2+BC2=AC2,则AB⊥BC,再由线面垂直的性质,得到BC⊥PA,即有BC⊥平面PAB,即可得证;
(2)设点D到平面PCB的距离为h,点F到平面BCD的距离是P点到平面BCD的距离的一半.VF-BCD=VD-BCF,
由棱锥的体积公式,即可求得.
| 3 |
(2)设点D到平面PCB的距离为h,点F到平面BCD的距离是P点到平面BCD的距离的一半.VF-BCD=VD-BCF,
由棱锥的体积公式,即可求得.
解答:
(1)证明:△ABC中,因为AC=4,BC=2,∠ACB=60°,
所以AB2=AC2+BC2-2AC•BC•cos60°=16+4-2×4×2×
=12,
即有AB=2
,由AB2+BC2=AC2,则AB⊥BC ,
,
又由PA⊥底面ABCD,得BC⊥PA,则BC⊥平面PAB,
故PB⊥BC;
(2)解:在△APC中,因为AF⊥PC,F为PC之中点,
所以AP=AC=4,PC=4
,PB=2
,
设点D到平面PCB的距离为h,
且点F到平面BCD的距离是P点到平面BCD的距离的一半.即
点F到平面BCD的距离为
PA=2,又VF-BCD=VD-BCF,
即
(
PA•S△BCD)=
S△BCFh,即2×
×4×
=
×
×4
h,
可求得:h=
,
则点D到平面PCB的距离为
.
所以AB2=AC2+BC2-2AC•BC•cos60°=16+4-2×4×2×
| 1 |
| 2 |
即有AB=2
| 3 |
 ,
,又由PA⊥底面ABCD,得BC⊥PA,则BC⊥平面PAB,
故PB⊥BC;
(2)解:在△APC中,因为AF⊥PC,F为PC之中点,
所以AP=AC=4,PC=4
| 2 |
| 7 |
设点D到平面PCB的距离为h,
且点F到平面BCD的距离是P点到平面BCD的距离的一半.即
点F到平面BCD的距离为
| 1 |
| 2 |
即
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
可求得:h=
2
| ||
| 7 |
则点D到平面PCB的距离为
2
| ||
| 7 |
点评:本题考查直线与平面垂直的性质和判定,考查点到平面的距离的求法,运用体积转换,考查棱锥的体积运算,属于中档题.

练习册系列答案
相关题目
若定义域在[0,1]的函数f(x)满足:
①对于任意x1,x2∈[0,1],当x1<x2时,都有f(x1)≥f(x2);
②f(0)=0;
③f(
)=
f(x);
④f(1-x)+f(x)=-1,
则f(
)+f(
)=( )
①对于任意x1,x2∈[0,1],当x1<x2时,都有f(x1)≥f(x2);
②f(0)=0;
③f(
| x |
| 3 |
| 1 |
| 2 |
④f(1-x)+f(x)=-1,
则f(
| 1 |
| 3 |
| 9 |
| 2014 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
